Weird Scientists

I just published the book "Weird Scientists". To see the rest of the characters in this series of blogs, go to Lulu.com and order the hardcover or download. My next series (and next book) is called "Divine Designers - the Creators of Geometry". The first blog in the series will follow in a few days.

Weird Scientist Number 3: Erwin Schrödinger

Schrödinger and his cat

“God knows I am no friend of probability theory, I have hated it from the first moment when our dear friend Max Born gave it birth. For it could be seen how easy and simple it made everything, in principle, everything ironed and the true problems concealed. Everybody must jump on the bandwagon [Ausweg]. And actually not a year passed before it became an official credo, and it still is[i].” [1]

- Erwin Schrödinger

Maybe Erwin Rudolf Josef Alexander Schrödinger did not care much for probability theory, but he could not avoid it when trying to formulate his wave theory—and the Schrödinger equation—for subatomic particles. Schrödinger (12 August 1887 – 4 January 1961) was a physicist and theoretical biologist who was one of the fathers of quantum mechanics, and is famed for a number of important contributions to physics, especially the Schrödinger equation, for which he received the Nobel Prize in Physics in 1933. In 1935, after extensive correspondence with friend Albert Einstein, he proposed the Schrödinger’s cat thought experiment[ii].

Life and Career

Early years

In 1887, Schrödinger was born in Vienna, Austria to Rudolf Schrödinger (cerecloth producer, botanist) and Georgine Emilia Brenda (daughter of Alexander Bauer, Professor of Chemistry, k.u.k. Technische Hochschule Vienna).

His mother was half-Austrian and half English; the English side of her family came from Leamington Spa. Schrödinger learned English and German almost at the same time because both were spoken in the family household. His father was a Catholic and his mother was a Lutheran.

In 1898, he attended the Akademisches Gymnasium. Between 1906 and 1910, Schrödinger studied in Vienna under Franz Serafin Exner[iii] (1849–1926) and Friedrich Hasenöhrl[iv] (1874–1915). He also conducted experimental work with Karl Wilhelm Friedrich (“Fritz”) Kohlrausch (1884–1953) [2]. In 1911, Schrödinger became an assistant to Exner. At an early age, Schrödinger was strongly influenced by Schopenhauer[v] [3]. As a result of his extensive reading of Schopenhauer’s works, he became deeply interested throughout his life in color theory, philosophy[vi], perception, and eastern religion, especially Hindu Vedānta [vii].
Middle years

In 1914, Erwin Schrödinger achieved Habilitation[viii] (venia legendi). Between 1914 and 1918, he participated in war work as a commissioned officer in the Austrian fortress artillery (Gorizia, Duino, Sistiana, Prosecco, and Vienna). On 6 April 1920, Schrödinger married Annemarie Bertel. The same year, he became the assistant to Max Wien, in Jena, and in September 1920, he attained the position of ao. Prof. (Ausserordentlicher Professor), roughly equivalent to Reader (UK) or associate professor (US), in Stuttgart. In 1921, he became o. Prof. (Ordentlicher Professor, i.e. full professor), in Breslau (now Wrocław, Poland).

In 1921, he moved to the University of Zürich. In January 1926, Schrödinger published in Annalen der Physik the paper “Quantisierung als Eigenwertproblem” [translation: “Quantization as an Eigenvalue Problem[ix]“] on wave mechanics and what is now known as the Schrödinger equation[x]. In this paper, he gave a “derivation” of the wave equation for time independent systems, and showed that it gave the correct energy eigenvalues for the hydrogen-like atom. This paper has been universally celebrated as one of the most important achievements of the twentieth century, and created a revolution in quantum mechanics, and indeed of all physics and chemistry. A second paper was submitted just four weeks later that solved the quantum harmonic oscillator[xi], the rigid rotor[xii] and the diatomic molecule[xiii], and gives a new derivation of the Schrödinger equation. A third paper in May showed the equivalence of his approach to that of Heisenberg and gave the treatment of the Stark effect[xiv]. A fourth paper in this most remarkable series showed how to treat problems in which the system changes with time, as in scattering problems. These papers were the central achievement of his career and were at once recognized as having great significance by the physics community.

In 1927, he succeeded Max Planck at the Friedrich Wilhelm University in Berlin. In 1933, however, Schrödinger decided to leave Germany; he disliked the Nazis‘ anti-Semitism. He became a Fellow of Magdalen College at the University of Oxford. Soon after he arrived, he received the Nobel Prize together with Paul Dirac. His position at Oxford did not work out; his unconventional personal life (Schrödinger lived with two women) [4] was not met with acceptance. In 1934, Schrödinger lectured at Princeton University; he was offered a permanent position there, but did not accept it. Again, his wish to set up house with his wife and his mistress may have posed a problem. He had the prospect of a position at the University of Edinburgh but visa delays occurred, and in the end, he took up a position at the University of Graz in Austria in 1936.

In the midst of these tenure issues in 1935, after extensive correspondence with friend Albert Einstein, he proposed the Schrödinger’s cat thought experiment.
Later years

In 1939, after the Anschluss[xv], Schrödinger had problems because of his flight from Germany in 1933 and his known opposition to Nazism. He issued a statement recanting this opposition (he later regretted doing so, and he personally apologized to Einstein). However, this did not fully appease the new dispensation and the university dismissed him from his job for political unreliability. He suffered harassment and received instructions not to leave the country, but he and his wife fled to Italy. From there he went to visiting positions in Oxford and Ghent Universities.

In 1940, he received a personal invitation from Ireland’s Taoiseach (prime minister) Éamon de Valera[xvi] to reside in Ireland and agree to help establish an Institute for Advanced Studies in Dublin. He moved to Clontarf, Dublin, became the Director of the School for Theoretical Physics, and remained there for 17 years, during which time he became a naturalized Irish citizen. He wrote about 50 further publications on various topics, including his explorations of unified field theory[xvii].

In 1944, he wrote, “What is Life?” In this book, Schrödinger discusses the limitations of science (physics) in explaining life: “We must therefore not be discouraged by the difficulty of interpreting life by the ordinary laws of physics. For that is just what is to be expected from the knowledge we have gained of the structure of living matter. We must also be prepared to find a new type of physical law prevailing in it. Or are we to term it a non-physical, not to say a super-physical, law?” [5] Though this limitation exists, the book contains a discussion of negentropy[xviii] and the concept of a complex molecule with the genetic code for living organisms. According to James D. Watson’s memoir, DNA, the Secret of Life, Schrödinger’s book gave Watson the inspiration to research the gene, which led to the discovery of the DNA double helix structure. Similarly, Francis Crick, in his autobiographical book What Mad Pursuit, described how he was influenced by Schrödinger’s speculations about how genetic information might be stored in molecules. However, the geneticist and 1946 Nobel-prize winner H. J. Muller had in his 1922 article “Variation due to Change in the Individual Gene” [6] already laid out all the basic properties of the heredity molecule that Schrödinger derives from first principles in What is Life?, properties which Muller refined in his 1929 article “The Gene As The Basis of Life” [7] and further clarified during the 1930s, long before the publication of What is Life? [225].

In Nature and the Greeks (1954), Schrödinger discusses the limitations of the physical world for supplying meaning to every aspect of existence or reality. He writes [8]:

“I am very astonished that the scientific picture of the real world around me is deficient. It gives a lot of factual information, puts all our experience in a magnificently consistent order, but it is ghastly silent about all and sundry that is really near to our heart, that really matters to us. It cannot tell us a word about red and blue, bitter and sweet, physical pain and physical delight; it knows nothing of beautiful and ugly, good or bad, God and eternity. Science sometimes pretends to answer questions in these domains, but the answers are very often so silly that we are not inclined to take them seriously.”

Schrödinger stayed in Dublin until retiring in 1955. During this time he remained committed to his particular passion; involvements with students occurred and he fathered two children by two different Irish women [1] [4]. He had a life-long interest in the Vedānta philosophy of Hinduism, which influenced his speculations at the close of “What is Life?” about the possibility that individual consciousness is only a manifestation of a unitary consciousness pervading the universe [9].

In 1956, he returned to Vienna (chair ad personam). At an important lecture during the World Energy Conference, he refused to speak on nuclear energy because of his skepticism about it and gave a philosophical lecture instead. During this period, Schrödinger turned from mainstream quantum mechanics‘ definition of wave-particle duality and promoted the wave idea alone causing much controversy.

Personal life

Schrödinger suffered from tuberculosis and several times in the 1920s stayed at a sanatorium in Arosa. It was there that he discovered his wave equation [10].

Schrödinger decided in 1933 that he could not live in a country in which persecution of Jews had become a national policy. Alexander Frederick Lindemann, the head of physics at Oxford University, visited Germany in the spring of 1933 to try to arrange positions in England for some young Jewish scientists from Germany. He spoke to Schrödinger about posts for one of his assistants and was surprised to discover that Schrödinger himself was interested in leaving Germany. Schrödinger asked for a colleague, Arthur March, to be offered a post as his assistant.
The request for March stemmed from Schrödinger’s unconventional relationships with women: although his relations with his wife Anny were good, he had had many lovers with his wife’s full knowledge (and in fact, Anny had her own lover, Hermann Weyl). Schrödinger asked for March to be his assistant because, at that time, he was in love with March’s wife Hilde.

Many of the scientists who had left Germany spent mid-1933 in the Italian province of South Tyrol. Here Hilde became pregnant with Schrödinger’s child. On 4 November 1933 Schrödinger, his wife and Hilde March arrived in Oxford. Schrödinger had been elected a fellow of Magdalen College. Soon after they arrived in Oxford, Schrödinger heard that, for his work on wave mechanics, he had been awarded the Nobel Prize.

In early 1934, Schrödinger was invited to lecture at Princeton University and while there, he was made an offer of a permanent position. On his return to Oxford, he negotiated about salary and pension conditions at Princeton but in the end, he did not accept. It is thought that the fact that he wished to live at Princeton with Anny and Hilde both sharing the upbringing of his child was not found acceptable. The fact that Schrödinger openly had two wives, even if one of them was married to another man, was not well received in Oxford either. Nevertheless, his daughter Ruth Georgie Erica was born there on 30 May 1934 [1].

On 4 January 1961, Schrödinger died in Vienna at the age of 73 of tuberculosis. He left a widow, Anny (born Annemarie Bertel on 3 December 1896, died 3 October 1965), and was buried in Alpbach, Austria.

Legacy

The philosophical issues raised by Schrödinger’s cat are still debated today and remains his most enduring legacy in popular science, while Schrödinger’s equation is his most enduring legacy at a more technical level. The huge crater Schrödinger, on the far side of the Moon is named after him. The Erwin Schrödinger International Institute for Mathematical Physics was established in Vienna in 1993.

Color

One of Schrödinger’s lesser-known areas of scientific contribution was his work on color, color perception, and colorimetry[xix] (Farbenmetrik). In 1920, he published three papers in this area:

· “Theorie der Pigmente von größter Leuchtkraft,” Annalen der Physik, (4), 62, (1920), 603-622
· “Grundlinien einer Theorie der Farbenmetrik im Tagessehen,” Annalen der Physik, (4), 63, (1920), 397-426; 427-456; 481-520 (Outline of a theory of color measurement for daylight vision)
· “Farbenmetrik,” Zeitschrift für Physik, 1, (1920), 459-466 (Color measurement).
The second of these is available in English as “Outline of a Theory of Color Measurement for Daylight Vision” in Sources of Color Science, Ed. David L. MacAdam, The MIT Press (1970), 134-182.

Works Cited

[1] Moore, Walter J., Schrödinger: Life and Thought. s.l. : Cambridge University Press, 1992. p. 222. ISBN-13: 978-0521437677 .
[2] Nobelprize.org., Erwin Schrödinger - Biography. The Nobel Prize in Physics 1933. [Online] The Nobel Foundation, 1933. [Cited: July 20, 2011.] http://nobelprize.org/nobel_prizes/physics/laureates/1933/schrodinger-bio.html.
[3] Moore, Walter J., A Life of Erwin Schrödinger. Abridged edition. s.l. : Cambridge University Press, 1994. ISBN-13: 978-0521469340.
[4] O'Connor, J. J. and Robertson, E. F., Erwin Rudolf Josef Alexander Schrödinger. School of Mathematics and Statistics, University of St Andrews, Scotland . 2003. http://www-history.mcs.st-andrews.ac.uk/Biographies/Schrodinger.html. Retrieved 20 July 2011..
[5] Schrödinger, Erwin., What is Life?: with "Mind and Matter" and "Autobiographical Sketches". s.l. : Cambridge University Press, 1992. ISBN-13: 978-0521427081.
[6] Meÿenn, Karl., "Schrödinger, Erwin Rudolf Josef Alexander." Neue Deutsche Biographie. online version, 2007, Vol. 23, pp. 578-580. http://www.deutsche-biographie.de/pnd118823574.html.
[7] Muller, H. J., The American Naturalist: V.56 1922. s.l. : University of Michigan Library, 2001 [1929]. ASIN: B002IKLF18 .
[8] Schrödinger, Erwin., 'Nature and the Greeks' and 'Science and Humanism'. s.l. : Cambridge University Press, 1996. ISBN-13: 978-0521575508.
[9] Schwartz, James., In Pursuit of the Gene. From Darwin to DNA. s.l. : Harvard University Press, 2008. ISBN-13: 978-0674026704.
[10] New World Encyclopedia., "Schrödinger, Erwin." New World Encyclopedia. April 24, 2008. http://www.newworldencyclopedia.org/entry/Erwin_Schr%C3%B6dinger.

Notes

[i] 13th of June, 1946, in a letter to Albert Einstein, as quoted by Walter Moore in Schrödinger: Life and Thought (1989) ISBN 0521437679
[ii] Schrödinger’s cat is a thought experiment (see Chapter 37), usually described as a paradox, that Austrian physicist Erwin Schrödinger devised in 1935. It illustrates what he saw as the problem of the Copenhagen interpretation of quantum mechanics applied to everyday objects. The thought experiment presents a cat that might be alive or dead, depending on an earlier random event. In the course of developing this experiment, he coined the term Verschränkung (entanglement).
[iii] Franz Serafin Exner (24 March 1849 - October 15, 1926) was an Austrian physicist.
[iv] Friedrich Hasenöhrl (November 30, 1874 - October 7, 1915) was an Austro-Hungarian physicist.
[v] Arthur Schopenhauer (22 February 1788 – 21 September 1860) was a German philosopher known for his pessimism and philosophical clarity.
[vi] In his lecture "Mind and Matter," Chapter 4, he said that a phrase "that has become familiar to us" is "The world extended in space and time is but our representation (Vorstellung)." This is a repetition of the first words of Schopenhauer’s main work.
[vii] Vedānta was originally a word used in Hindu philosophy as a synonym for that part of the Veda texts known also as the Upanishads.
[viii] Habilitation is the highest academic qualification a scholar can achieve by his or her own pursuit in several European and Asian countries. Earned after obtaining a research doctorate, such as a Ph.D., habilitation requires the candidate to write a professorial thesis (often known as a Habilitationsschrift, or Habilitation thesis) based on independent scholarship, reviewed by and defended before an academic committee in a process similar to that for the doctoral dissertation. However, the level of scholarship has to be considerably higher than that required for a research doctoral (Ph.D.) thesis in terms of quality and quantity, and must be accomplished independently, in contrast with a Ph.D. dissertation typically directed or guided by a faculty supervisor.
[ix] The eigenvectors of a square matrix are the non-zero vectors that, after being multiplied by the matrix, remain proportional to the original vector (i.e., change only in magnitude, not in direction). For each eigenvector, the corresponding eigenvalue is the factor by which the eigenvector changes when multiplied by the matrix. The prefix eigen- is adopted from the German word "eigen" for "own" in the sense of a characteristic description. The eigenvectors are sometimes also called characteristic vectors. Similarly, the eigenvalues are also known as characteristic values.
[x] The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics, specifically quantum mechanics, it is an equation that describes how the quantum state of a physical system changes in time. In the standard interpretation of quantum mechanics, the quantum state, also called a wavefunction or state vector, is the most complete description that can be given to a physical system. Solutions to Schrödinger’s equation describe not only molecular, atomic and subatomic systems, but also macroscopic systems, possibly even the whole universe.
[xi] The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics. Furthermore, it is one of the few quantum-mechanical systems for which a simple, exact solution is known.
[xii] The rigid rotor is a mechanical model that is used to explain rotating systems. An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space three angles are required. A special rigid rotor is the linear rotor that is a 2-dimensional object, requiring two angles to describe its orientation. An example of a linear rotor is a diatomic molecule. More general molecules like water (asymmetric rotor), ammonia (symmetric rotor), or methane (spherical rotor) are 3-dimensional, see classification of molecules.
[xiii] Diatomic molecules are molecules composed only of two atoms, of either the same or the different chemical elements. The prefix di- means two in Greek. Common diatomic molecules are hydrogen (H2), nitrogen (N2), oxygen (O2), and carbon monoxide (CO). Seven elements exist in the diatomic state in the liquid and solid forms: H2 , N2, O2, F2, Cl2, Br2, and I2. Most elements (and many chemical compounds) aside from these form diatomic molecules when evaporated, although at very high temperatures, all materials disintegrate into atoms. The noble gases do not form diatomic molecules.
[xiv] The Stark effect (named after Johannes Starck)is the shifting and splitting of spectral lines of atoms and molecules due to the presence of an external static electric field. The amount of splitting and or shifting is called the Stark splitting or Stark shift.
[xv] The Anschluss (spelled Anschluß at the time of the event, and until the German orthography reform of 1996; German for "link-up"), also known as the Anschluss Österreichs, was the occupation and annexation of Austria into Nazi Germany in 1938.
[xvi] Éamon de Valera(14 October 1882 – 29 August 1975) was one of the dominant political figures in twentieth century Ireland, serving as head of government and head of state and introducing the Constitution of Ireland. De Valera was a leader of Ireland’s struggle for independence from Britain in the Irish War of Independence and of the anti-Treaty forces in the ensuing Irish Civil War (1922–23). In 1926, he founded Fianna Fáil and was head of government from 1932–48, 1951–54 and 1957–59 and President of Ireland from 1959–73.
[xvii] Since the 19th century, some physicists have attempted to develop a single theoretical framework that can account for the fundamental forces of nature—a unified field theory. Classical unified field theories are attempts to create a unified field theory based on classical physics. In particular, unification of gravitation and electromagnetism was actively pursued by several physicists and mathematicians in the years between World War I and World War II. This work spurred the purely mathematical development of differential geometry. Albert Einstein is the best known of the many physicists who attempted to develop a classical unified field theory.
[xviii] The negentropy, also negative entropy or syntropy, of a living system is the entropy that it exports to keep its own entropy low; it lies at the intersection of entropy and life. The concept and phrase "negative entropy" were introduced by Erwin Schrödinger in his 1943 popular-science book What is Life?
[xix] Colorimetry is "the science and technology used to quantify and describe physically the human color perception."

Weird Scientist Number 2: Satyendra Nath Bose

"Perhaps Satyen Bose’s greatest charm lies in his ability to look at life in a total manner. The minor pleasure of leisure and pleasant company were to him a part of a bigger universe of the pleasures of the mind and the intellect. In a sense this was also his strongest limitation. Bose was a man who tried to see the world around him in its entirety, in its complexity and in which his particular science and himself were small parts."

B. D. Nag Chaudhuri

Satyendra Nath Bose (1 January 1894 – 4 February 1974), FRS, was an Indian mathematician and physicist noted for his collaboration with Albert Einstein in developing a theory regarding the gaslike qualities of electromagnetic radiation. He is best known for his work on quantum mechanics in the early 1920s, providing the foundation for Bose–Einstein statistics and the theory of the Bose–Einstein condensate. He is honoured as the namesake of the boson (bosonparticle.com, 2011). He was awarded India's second highest civilian award, the Padma Vibhushan in 1954 by the Government of India (NIC, 2005).

Satyendra Nath Bose in Paris 1925

Although more than one Nobel Prize was awarded for research related to the concepts of the boson, Bose–Einstein statistics and Bose–Einstein condensate—the latest being the 2001 Nobel Prize in Physics, which was given for advancing the theory of Bose–Einstein condensates—Bose himself was not awarded the Nobel Prize. Among his other talents, Bose spoke several languages and could also play the esraj, a musical instrument similar to a violin.

In his book, The Scientific Edge, the noted physicist Jayant Narlikar observed (Narlikar, 2003):

“S. N. Bose’s work on particle statistics (c. 1922), which clarified the behaviour of photons (the particles of light in an enclosure) and opened the door to new ideas on statistics of Microsystems that obey the rules of quantum theory, was one of the top ten achievements of 20th century Indian science and could be considered in the Nobel Prize class.”

Early life and career

Bose was born in Calcutta, British India, the eldest of seven children. His father, Surendranath Bose, worked in the Engineering Department of the East Indian Railway Company. Bose attended Hindu School in Calcutta, and later attended Presidency College, also in Calcutta, earning the highest marks at each institution. He came in contact with teachers such as Jagadish Chandra Bose and Prafulla Chandra Roy who provided inspiration to aim high in life. From 1916 to 1921 he was a lecturer in the physics department of the University of Calcutta. In 1921, he joined the department of Physics of the then recently founded Dhaka University (now in Bangladesh and called University of Dhaka) (BANC, 2011).

In 1924, while working as a Reader at the Physics Department of the University of Dhaka, Bose wrote a paper deriving Planck's quantum radiation law without any reference to classical physics and using a novel way of counting states with identical particles. This paper was seminal in creating the very important field of quantum statistics. After initial setbacks to his efforts to publish, he sent the article directly to Albert Einstein in Germany. Einstein, recognizing the importance of the paper, translated it into German himself and submitted it on Bose's behalf to the prestigious Zeitschrift für Physik. As a result of this recognition, Bose was able to leave India for the first time and spent two years in Europe, during which he worked with Louis de Broglie, Marie Curie, and Einstein (Grigrious, 2010).

After his stay in Europe, Bose returned to Dhaka in 1926. He became a professor and was made head of the Department of Physics, and continued teaching at Dhaka University until 1945. He was also Dean of the Faculty of Science at Dhaka University for a long period. When the partition of India became imminent, he returned to Calcutta and taught at Calcutta University until 1956, when he retired and was made professor emeritus (Chatterjee & Chatterjee, 2002).

Bose–Einstein statistics

Bose was an ardent follower of Einstein’s ideas and decided to attempt another derivation of Planck’s law of radiation without using any Maxwellian wave theory of radiation. He had read Planck’s work on the distribution of energy from a black body based on this new theory. Satyendra Nath had always been a perfectionist and would not accept any ad hoc assumption while working out a theory. So he was not happy with Planck’s derivation which had such ad hoc assumptions (Chatterjee & Chatterjee, 2002).

While presenting a lecture at the University of Dhaka on the theory of radiation and the ultraviolet catastrophe, Bose attempted a statistical explanation of the interaction of atoms and radiation using the principle, recently developed by Werner Heisenberg, of uncertainty concerning the characteristics of electrons around the atomic nucleus (Walker A. R., 2011). During this lecture, Bose committed an error in applying the theory, which unexpectedly gave a prediction that agreed with the experiment. He adapted this lecture into a short paper called “Planck's Law and the Hypothesis of Light Quanta”.

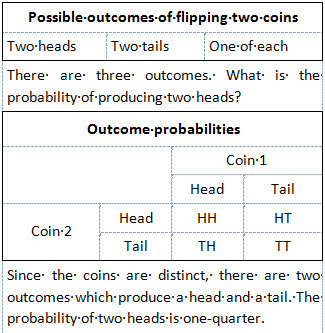
The error was a simple mistake—similar to arguing that flipping two fair coins will produce two heads one-third of the time—that would appear obviously wrong to anyone with a basic understanding of statistics. However, the results it predicted agreed with experiment, and Bose realized it might not be a mistake at all. He for the first time took the position that the Maxwell–Boltzmann distribution would not be true for microscopic particles where fluctuations due to Heisenberg's uncertainty principle will be significant. Thus he stressed the probability of finding particles in the phase space, each state having volume , and discarding the distinct position and momentum of the particles (Grigrious, 2010).

When Bose sent his paper to Philosophical Magazine (Chatterjee & Chatterjee, 2002) for publication it was rejected because the editors thought he had made a simple mistake in his calculations. So he sent a copy to Einstein, soliciting his opinion. (Walker A. R., 2011). Here is what Bose wrote in his first letter to Einstein (Chatterjee & Chatterjee, 2002):

“I have ventured to send you the accompanying article for your perusal and opinion. I am anxious to know what you think of it. You will see that I have tried to deduce the coefficient in Planck’s laws, independent of the classical electrodynamics, only assuming that the ultimate elementary regions in the phase space had the content . I do not know sufficient German to translate the paper. If you think the paper worth publication, I shall be grateful if you arrange for its publication in Zeitschrift fur Physik. Though a complete stranger to you, I do not feel any hesitation in making such a request. Because we are all your pupils though profiting only by your teachings through your writings. I do not know whether you still remember that somebody from Calcutta asked your permission to translate your papers on relativity in English. You acceded to the request. The book has since been published. I was the one who translated your paper ‘Generalised Relativity’.”

Einstein approved. His theory finally achieved respect when Einstein sent his own paper in support of Bose's to Zeitschrift für Physik, asking that they be published together (Walker A. R., 2011). This was done in 1924. Very soon the paper was published, translated by Einstein, and with the following translator’s remark (Chatterjee & Chatterjee, 2002):

“In my opinion Bose’s derivation of the Planck formula signifies an important development. The method considered here yields also the quantum theory of ideal gases which I shall discuss elsewhere.”

The reason Bose's "mistake" produced accurate results was that since photons are indistinguishable from each other, one cannot treat any two photons having equal energy as being two distinct identifiable photons. By analogy, if in an alternate universe coins were to behave like photons and other bosons, the probability of producing two heads would indeed be one-third ( ). But what Bose actually did was more than derive a formula. He introduced new concepts in physics Bose's "error" (Grigrious, 2010), later named as Bose Statistics. Einstein understood the significance of it and immediately applied it to the case of ideal gas and found a new relation known as Bose-Einstein Statistics (Chatterjee & Chatterjee, 2002).

Einstein adopted the idea and extended it to atoms. This led to the prediction of the existence of phenomena which became known as Bose-Einstein condensate, a dense collection of bosons (which are particles with integer spin, named after Bose), which was demonstrated to exist by experiment in 1995 (Grigrious, 2010).

Later work

Bose's ideas were afterwards well received in the world of physics, and he was granted leave from the University of Dhaka to travel to Europe in 1924 (Grigrious, 2010). He spent a year in France and worked with Marie Curie, and met several other well-known scientists. He then spent another year abroad, working with Einstein in Berlin. Upon his return to Dhaka, he was made a professor in 1926. He did not have a doctorate, and so ordinarily he would not be qualified for the post, but Einstein recommended him. His work ranged from X-ray crystallography to unified field theories. He also published an equation of state for real gases with Megh Nad Saha (Chatterjee & Chatterjee, 2002).

When Satyendra Nath returned to Dacca from Europe in 1926, the post of the professor of physics at the Dacca University was vacant. The selection committee recommended the name of D.M. Bose as its first choice and that of S.N. Bose as its alternative choice. D.M. Bose was then the Ghose professor of physics at Calcutta. He was comfortably settled in his research work and was also in close touch with his uncle, Sir J.C Bose and his research laboratory, the Bose Institute, adjacent to the University College of Science and Technology. Since D.M. Bose did not accept the position offered to him by the Dacca University, Satyendra Nath became the professor of physics at Dacca University, where he continued till 1945 (Chatterjee & Chatterjee, 2002).

Apart from physics he did some research in biochemistry and literature (Bengali, English). He made deep studies in chemistry, geology, zoology, anthropology, engineering and other sciences. Being an Indian of Bengali descent, he devoted a lot of time to promoting Bengali as a teaching language, translating scientific papers into it, and promoting the development of the region (Grigrious, 2010).

In 1944 Bose was elected General President of the Indian Science Congress. In 1958 he became a Fellow of the Royal Society.

Works Cited

BANC. (2011). Satyendra Nath Bose . Retrieved August 1, 2011, from Bengali Association of North Carolina: www.banc-online.org/pdfs/SNB.pdf

bosonparticle.com. (2011). Articles about boson particle. Retrieved August 1, 2011, from Boson Particle: http://www.bosonparticle.com/articles

Chatterjee, S., & Chatterjee, E. (2002). Satyendra Nath Bose. National Book Trust.

Grigrious, V. I. (2010, February). Satyendra Nath Bose. Bhouthika Jyothi, 6(Ruby Jubilee Special), p. 41.

Narlikar, J. V. (2003). The Scientific Edge. Penguin Books.

NIC. (2005). Padma Vibhushan Awardees. (National Informatics Centre, Government of India.) Retrieved August 1, 2011, from india.gov.in: http://india.gov.in/myindia/padmavibhushan_awards_list1.php?start=250

Walker, A. R. (2011). From black bodies to bar codes: lasers. In Magical inventions or the art of discovery. Unpublished.

Weird Scientis Number 1: Clinton Davisson

This is the first in a series of blogs featuring the creators of Quantum Mechanics/Theory. These weird scientists (in the most respectable sense) are part of my not-yet-published book "Weird Scientists (not to be confuses with "Weird Science", a 1985 American teen fantasy comedy film).

Clinton Davisson

“We think we understand the regular reflection of light and X rays - and we should understand the reflections of electrons as well if electrons were only waves instead of particles ... It is rather as if one were to see a rabbit climbing a tree, and were to say ‘Well, that is rather a strange thing for a rabbit to be doing, but after all there is really nothing to get excited about. Cats climb trees—so that if the rabbit were only a cat, we would understand its behavior perfectly.’ Of course, the explanation might be that what we took to be a rabbit was not a rabbit at all but was actually a cat. Is it possible that we are mistaken all this time in supposing they are particles, and that actually they are waves?”

- Clinton Davisson

Clinton Joseph Davission (October 22, 1881 – February 1, 1958) studied the properties of subatomic particles, not cats or rabbits. Davisson was an American physicist who won the 1937 Nobel Prize in Physics for his discovery of electron diffraction. Davisson shared the Nobel Prize with George Paget Thomson, who independently discovered electron diffraction at about the same time as Davisson. Their results provided poof for Louis de Broglie's pioneering theory of wave-particle duality in quantum mechanics.

Biography

Early years

Davisson was born in Bloomington, Illinois, on 22 October 1881, the first of two children. His father, Joseph, who had settled in Bloomington after serving in the Civil War, was a contract painter and paperhanger by trade. His mother, Mary, occasionally taught in the Bloomington school system. Their home was, as Davisson's sister, Carrie, characterized it, "a happy congenial one—plenty of love but short on money."

Davisson, slight of frame and frail throughout his life, graduated from high school at age 20, in 1902. For his proficiency in mathematics and physics, he received a one-year scholarship to the University of Chicago; his six-year career there was interrupted several times for lack of funds. He acquired his love and respect for physics from Robert Millikan[i]; Davisson was "delighted to find that physics was the concise, orderly science [he] had imagined it to be, and that a physicist [Millikan] could be so openly and earnestly concerned about such matters as colliding bodies" (Gehrenbeck, 1978).

In 1905, upon the recommendation of Millikan, Davisson was hired by Princeton University as Instructor of Physics. He completed the requirements for his B.S. degree from Chicago in 1908, mainly by working in the summers. While teaching at Princeton, he did doctoral thesis research with Owen Richardson[ii]. He received his Ph.D. in physics from Princeton in 1911; in the same year he married Richardson's sister, Charlotte (Kelly, 1962) (Nobelprize.org, 1937).

Career

Before finishing his undergraduate degree at Chicago, he became a part-time instructor in physics at Princeton University, where he came under the influence of the British physicist Richardson, who was directing electronic research there. Davisson's PhD thesis at Princeton, in 1911, extended Richardson's research on the positive ions emitted from salts of alkaline metals. Davisson later credited his own success to having caught "the physicist's point of view—his habit of mind—his way of looking at things" from such men as Millikan and Richardson (Kelly, 1962).

After completing his degree, Davisson married Richardson's sister, Charlotte, who had come from England to visit her brother. After a honeymoon in Maine, Davisson joined the Carnegie Institute of Technology in Pittsburgh as an instructor in physics. The 18-hour-per-week teaching load left little time for research, and in six years there he published only three short theoretical notes. One notable break during this period was the summer of 1913, when Davisson worked with J. J. Thomson at the Cavendish laboratory in England.

Davisson was then appointed as an assistant professor at the Carnegie Institute of Technology. In April 1917, he was refused enlistment in the United States Army, because of his frailty (MacRae, 1972). In June of the same year he accepted war-time employment in the Engineering Department of the Western Electric Company (later Bell Telephone Laboratories), New York City—at first for summer, then, on leave of absence from Carnegie Tech., for the duration of the World War. His work was to develop and test oxide-coated nickel filaments to serve as substitutes for the oxide-coated platinum filaments then in use. At the end of the war, he resigned an assistant professorship to which he had been appointed at Carnegie Tech. to continue as a Member of the Technical Staff of the Telephone Laboratories (Nobelprize.org, 1937).

At the end of the war, Davisson accepted a permanent position at Western Electric after receiving assurances of his freedom there to do basic research. He had found that his teaching responsibilities at the Carnegie Institute largely precluded him from doing research (Kelly, 1962). The assignment that engaged Davisson and Lester Germer in their first joint effort reflects one of the chief interests of the parent company, AT&T, at this time: to conduct a fundamental investigation into the role of positive-ion bombardment in electron emission from oxide-coated cathodes. They published their results in the Physical Review in 1920, concluding that positive-ion bombardment has a negligible effect on the electron emission from oxide-coated cathodes (C. J. Davisson, 1920).

Davisson remained at Western Electric (and Bell Telephone) until his formal retirement in 1946. He then accepted a research professor appointment at the University of Virginia that continued until his second retirement in 1954 (Kelly, 1962).

Electron Diffraction and the Davisson-Germer Experiment

“Discoveries in physics are made when the time for making them is ripe, and not before.” (Davisson, 1965)

- Clinton Davisson

The Davisson–Germer experiment was a physics experiment conducted by American physicists Clinton Davisson and Lester Germer in 1927, which confirmed the de Broglie hypothesis. The de Broglie hypothesis says that particles of matter (such as electrons) have wave properties. This demonstration of wave–particle duality was important historically in the establishment of quantum mechanics and of the Schrödinger equation.

The experiment consisted of firing an electron beam from an electron gun on a nickel crystal at normal incidence (i.e. perpendicular to the surface of the crystal). The electron gun consisted of a heated filament that released thermally excited electrons, which were then accelerated through a potential difference of 54 V, giving them a kinetic energy of 54 eV. An electron detector was placed at an angle to obtain a maximum reading, and measured the number of electrons that were scattered at that particular angle (Germer, 1964) (Eisberg & Resnick, 1985).

Davisson, Germer and Calbick in 1927, the year they demonstrated electron diffraction. In their New York City laboratory are Clinton Davisson, age 46; Lester Germer, age 31, and their assistant Chester Calbick, age 23. Germer, seated at the observer's desk, appears ready to read and record electron current from the galvanometer[iii] (seen beside his head); the banks of dry cells behind Davisson supplied the current for the experiments.

Diffraction is a characteristic effect when a wave is incident upon an aperture or a grating, and is closely associated with the meaning of wave motion itself. In the 19th Century, diffraction was well-established for light and for ripples on the surfaces of fluids. In 1927, while working for Bell Labs, Davisson and Germer performed their famous experiment showing that electrons were diffracted at the surface of a crystal of nickel. This celebrated Davisson-Germer experiment confirmed the de Broglie hypothesis that particles of matter have a wave-like nature, which is a central tenet of quantum mechanics. In particular, their observation of diffraction allowed the first measurement of a wavelength for electrons. The measured wavelength agreed well with de Broglie's equation , where is Planck's constant and is the electron's momentum (Germer, 1964) (Davisson, 1965).

The sixth of January 1927 might well be regarded as the birthday of electron waves, for it was the day that data directly supporting the de Broglie hypothesis of electron waves were first observed. Note the peak deflection at 65 volts, and the detailed study of the region directly below. Calbick's handwriting is neat and cautious; Germer's is bold and expansive. Davisson made no entries in any of the research notebooks kept in the Bell Labs files.

Davisson and Germer succeeded where others had failed. In fact, the others (Walter Elsasser, E. G. Dymond, Patrick Blackett, James Chadwick and Charles Ellis), who had the idea of electron diffraction considerably ahead of Davisson and Germer, were not able to produce the desired experimental evidence for it. George Paget Thomson, who did find that evidence by a very different method, testified to the magnitude of the technical achievement as follows (Thomson, 1961):

"[Davisson and Germer's work] was indeed a triumph of experimental skill. The relatively slow electrons [they] used are most difficult to handle. If the results are to be of any value the vacuum has to be quite outstandingly good. Even now [1961] ... it would be a very difficult experiment. In those days it was a veritable triumph. It is a tribute to Davisson's experimental skill that only two or three other workers have used slow electrons successfully for this purpose."

From 1930-1937, Davisson devoted himself to the study of the theory of electron optics[iv] and to applications of this theory to engineering problems. He then investigated the scattering and reflection of very slow electrons by metals. During World War II he worked on the theory of electronic devices and on a variety of crystal physics[v] problems.

In 1946 he retired from Bell Telephone Laboratories after 29 years of service. From 1947 to 1949, he was Visiting Professor of Physics at the University of Virginia, Charlottesville, Va.
The National Academy of Sciences awarded Davisson the Comstock Prize in 1928. In 1931 Franklin Institute awarded him the Elliott Cresson Medal, and in 1935 the Royal Society (London) awared him the Hughes Medal. In 1941, the University of Chicago awarded him the Alumni Medal. He held honorary doctorates from Purdue University, Princeton University, the University of Lyon and Colby College.

Personal life

In 1911, Clinton married Charlotte Sara Richardson, a sister of Professor Richardson. Clinton and Charlotte Davisson had four children, including the American physicist Richard Davisson. Clinton died in Charlottesville on February 1, 1958, at the age of 76, and was survived by his wife, three sons and one daughter. The crater Davisson on the Moon is named after him.

Notes

[i] Robert A. Millikan (22 March 1868 – 19 December 1953) was an American experimental physicist, and Nobel laureate in physics for his measurement of the charge on the electron and for his work on the photoelectric effect. He served as president of Caltech from 1921 to 1945. He also served on the board of trustees for Science Service, now known as Society for Science & the Public, from 1921-1953.
[ii] Sir Owen Willans Richardson, FRS (26 April 1879 - 15 February 1959) was a British physicist who won the Nobel Prize in Physics in 1928 for his work on thermionic emission, which led to Richardson's Law—the current from a heated wire seemed to depend exponentially on the temperature of the wire.
[iii] A galvanometer is a type of ammeter: an instrument for detecting and measuring electric current. It is an analog electromechanical transducer that produces a rotary deflection of some type of pointer in response to electric current flowing through its coil. The term has expanded to include uses of the same mechanism in recording, positioning, and servomechanism equipment.
[iv] Electron optics deals with the focusing and deflection of electrons using magnetic and/or electrostatic fields.
[v] Chystal physics (physical crystallography), is the study of the physical properties of crystals and crystalline aggregates and changes in the properties under the influence of various factors.

Works Cited

C. J. Davisson, L. H. (1920). Physics Review, 15, p. 330.

Davisson, C. (1965). The Discovery of Electron Waves. In P. 1.-1. Nobel Lectures. Amsterdam: Elsevier Publishing Company.

Eisberg, R., & Resnick, R. (1985). Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles (2nd ed.). New York: John Wiley & Sons.

Gehrenbeck, R. K. (1978, January). Electron diffraction:fifty years ago. Physics Today.Germer, L. H. (1964, July). Low-Energy Electron Diffraction. Physics Today, pp. 19-23.

Kelly, M. J. (1962). Clinton Joseph Davisson. In Biographical Memoirs Vol. XXXVI (pp. 52-79). New York: Columbia University Press.MacRae, A. U. (1972, January).

Lester H. Germer - Obituary. Physics Today, pp. 93-97.Nobelprize.org. (1937). Clinton Davisson - Biography. The Nobel Prize in Physics 1937.

Thomson, G. P. (1961). The Inspiration of Science. London: Oxford U.P.

General Relativity (excerpt from Albert Einstein: "Nobody expected me to lay golden eggs"

“The general theory of relativity is as yet incomplete insofar as it has been able to apply the general principle of relativity satisfactorily only to gravitational fields, but not to the total field. We do not yet know with certainty, by what mathematical mechanism the total field in space is to be described and what the general invariant laws are to which this total field is subject. One thing, however, seems certain: namely, that the general principle of relativity will prove a necessary and effective tool for the solution of the problem of the total field.”

- Albert Einstein, “The theory of relativity” 1949 [1]

Introduction to General Relativity

General relativity was Einstein’s theory of gravity, published in 1915 [2], which extended special relativity to take into account non-inertial frames of reference—areas that are accelerating with respect to each other. General relativity takes the form of field equations, describing the curvature of space-time and the distribution of matter throughout space-time. The effects of matter and space-time on each other are what we perceive as gravity.

The theory of the space-time continuum already existed, but under general relativity, Einstein was able to describe gravity as the bending of space-time geometry. Einstein defined a set of field equations, which represented the way that gravity behaved in response to matter in space-time. Physicists could use these field equations to represent the geometry of space-time that was at the heart of the theory of general relativity.

As Einstein developed his general theory of relativity, he had to refine the accepted notion of the space-time continuum into a more precise mathematical framework. He also introduced another principle, the principle of covariance. This principle states that the laws of physics must take the same form in all coordinate systems. In other words, all space-time coordinates are treated the same by the laws of physics—in the form of Einstein’s field equations. This is similar to the relativity principle, which states that the laws of physics are the same for all observers moving at constant speeds. In fact, after general relativity was developed, it was clear that the principles of special relativity were a special case.

Einstein’s basic principle was that no matter where you are—Toledo, Mount Everest, Jupiter, or the Andromeda galaxy—the same laws apply. This time, though, the laws were the field equations, and your motion could very definitely impact what solutions came out of the field equations. Applying the principle of covariance meant that the space-time coordinates in a gravitational field had to work exactly the same way as the space-time coordinates on a spaceship that was accelerating. If you are accelerating through empty space—where the space-time field is flat, as in the left picture of this figure—the geometry of space-time would appear to curve. This meant that if there is an object with mass generating a gravitational field, it had to curve the space-time field as well (as shown in the right picture of the figure).

Without matter, space-time is flat (left), but it curves when matter is present (right).

In other words, Einstein had succeeded in explaining the Newtonian mystery of where gravity came from! Gravity resulted from massive objects bending space-time geometry itself.
Because space-time curved, the objects moving through space would follow the “straightest” path along the curve, which explains the motion of the planets. They follow a curved path around the sun because the sun bends space-time around it.

Again, you can think of this by analogy. If you are flying by plane on Earth, you follow a path that curves around the Earth. In fact, if you take a flat map and draw a straight line between the start and end points of a trip, that would not be the shortest path to follow. The shortest path is actually the one formed by a “great circle” that you’d get if you cut the Earth directly in half, with both points along the outside of the cut. Traveling from New York City to northern Australia involves flying up along southern Canada and Alaska—nowhere close to a straight line on the flat maps we are used to.

Similarly, the planets in the solar system follow the shortest paths—those that require the least amount of energy—and that results in the motion we observe.

In 1911, Einstein had done enough work on general relativity to predict how much the light should curve in this situation, which should be visible to astronomers during an eclipse [3].

When he published his complete theory of general relativity in 1915, Einstein had corrected a couple of errors [249]. In 1919, an expedition set out to observe the deflection of light by the sun during an eclipse, in to the west African island of Principe. The expedition leader was British astronomer Arthur Eddington, a strong supporter of Einstein [3].

Eddington returned to England with the pictures he needed, and his calculations showed that the deflection of light precisely matched Einstein’s predictions. General relativity had made a prediction that matched observation.

Albert Einstein had successfully created a theory that explained the gravitational forces of the universe and had done so by applying a handful of basic principles. To the degree possible, the work had been confirmed, and most of the physics world agreed with it. Almost overnight, Einstein’s name became world famous. In 1921, Einstein traveled through the United States to a media circus that probably was not matched until the Beatlemania of the 1960s [4].



References

[1] Einstein, Albert., The Theory Of Relativity . s.l. : Citadel, 2000 [1949]. ISBN-13: 978-0806517650.

[2] Einstein, Albert., "Die Feldgleichungen der Gravitation." Sitzungsberichte der Preussischen Akademie der Wissenschaften zu Berlin. November 25, 1915, pp. 844–847. http://nausikaa2.mpiwg-berlin.mpg.de/cgi-bin/toc/toc.x. cgi?dir=6E3MAXK4&step=thumb.

[3] Einstein, Albert., "Über den Einfluß der Schwerkraft auf die Ausbreitung des Lichtes (About the influence of gravity on the propagation of light )." Annalen der Physik. 1911, Vol. 340, 10. translated "On the Influence of Gravitation on the Propagation of Light" in The collected papers of Albert Einstein. Vol. 3 : The Swiss years: writings, 1909–1911 (Princeton University Press, Princeton, NJ, 1994), Anna Beck translator.

[4] Pais, Abraham., Subtle is the Lord. The Science and the Life of Albert Einstein. s.l. : Oxford University Press, 1982. pp. 382–386. ISBN 019853907X

Using Math to Defeat the Enemy

Preface

Many of the criticisms directed towards military simulations derive from an incorrect application of them as a predictive and analytical tool. The outcome supplied by a model relies to a greater or lesser extent on human interpretation and therefore should not be regarded as providing a ‘gospel’ truth. However, most game theorists and analysts generally understand this, it can be tempting for a layman—for example, a politician who needs to present a 'black and white' situation to his electorate—to settle on an interpretation that supports his preconceived position. Tom Clancy, in his novel Red Storm Rising, illustrated this problem when one of his characters, attempting to persuade the Soviet Politburo that the political risks of war with NATO were acceptable, used as evidence the results of a simulation carried out to model just such an event. It is revealed in the text that there were in fact three sets of results from the simulation; a best-, intermediate- and worst-case outcome. The advocate of war chose to present only the best-case outcome, thus distorting the results to support his case (Clancy, 1988).

There have been many charges over the years of computerized models being unrealistic and slanted towards a particular outcome. Critics point to the case of military contractors, seeking to sell a weapons system. For obvious reasons of cost, weapons systems (such as an air-to-air missile system for use by fighter aircraft) are modeled extensively on computers. Without testing of their own, a potential buyer must rely to a large extent on the manufacturer's own model. This might well indicate a very effective system, with a high kill probability (Pk). However, it may be the model was configured to show the weapons system under ideal conditions, and its actual operational effectiveness will be somewhat less than stated. The US Air Force quoted their AIM-9 Sidewinder missile as having a Pk of 0.98 (it will successfully destroy 98% of targets it is fired at). In operational use during the Falklands War in 1982, the British recorded its actual Pk as 0.78 (Allen T. B., 1987).

Human factors have been a constant thorn in the side of the designers of military simulations. Whereas political-military simulations are often required by their nature to grapple with what modelers refer to as "soft" problems, purely military models often seem to prefer to concentrate on hard numbers. While a warship can be regarded, from the perspective of a model, as a single entity with known parameters (speed, armor, gun power, and the like), land warfare often depends on the actions of small groups or individual soldiers where training, morale, intelligence, and personalities (leadership) come into play. For this reason, it is more taxing to model—there are many difficult-to-formulate variables. One valid criticism of some military simulations is these nebulous human factors are often ignored (partly because they are so hard to model accurately). Other perplexing issues include aggregation-disaggregation, communication networks, attrition, and end-game modeling.

“Using Math to Defeat the Enemy: Combat Modeling for Simulation” is intended to provide a foundation in the underlying combat modeling issues of military simulations. Of course, this is just a background, and a more rigorous treatment can be found in my book, Mathematical Modeling of Warfare and Combat Phenomenon (2011), Lulu.com, ISBN 978-1-4583-9255-8. Ultimately, this is a resource/reference book covering a wide gambit of military modeling issues.
This book is organized in two parts: Simulation (Part I) and Modeling (Part II). There are numerous practical applications and example models used in past and current military simulations.

This book is a result of about 25 years of use, application, research, and teaching military modeling and simulation. Much of the material in this book based on practical experience with modeling and simulation and extraction of my course notes from PowerPoint presentations.

Jeffrey S. Strickland, Ph.D.
CMSP, ASEP
President
Simulation Educators
Colorado Springs, Co
www.simulation-educators.com

Chaos Theory for Beginners (excerpt from Quantum Phaith)

It’s a Jungle Out There [1]

"The whole history of science has been the gradual realization that events do not happen in an arbitrary manner, but that they reflect a certain underlying order, which may or may not be divinely inspired."

- Stephen Hawking

Life finds a way

Remember Jurassic Park? Handsome mathematician Doctor Ian Malcolm[2] (pictured here [6]) explaining to pretty Doctor Sattler why he thought it was unwise to have T-rexes and the likes romping around on an island? John Hammond, the annoying owner, promised that nothing could go wrong and that all precautions were taken to ensure the safety of visitors. Dr. Malcolm did not agree. "Life finds a way," he said.

Nature is highly complex, and the only prediction you can make is that she is unpredictable. The amazing unpredictability of nature is what Chaos Theory looks at. Why? Because, nature is marvelous and mysterious instead of being boring and translucent. Chaos Theory has managed to somewhat capture the beauty of the unpredictable and display it in the most awesome patterns. Nature, when looked upon with the right kind of eyes, presents herself as one of the most fabulous works of art ever wrought.

What is Chaos Theory?

Chaos Theory is a mathematical sub-discipline that studies complex systems. Examples of the complex systems that Chaos Theory helped fathom are earth's weather system, the behavior of water boiling on a stove, migratory patterns of birds, or the spread of vegetation across a continent. Chaos is everywhere, from nature's most intimate considerations to art of any kind. Chaos-based graphics show up all the time, wherever flocks of little space ships sweep across the movie screen in highly complex ways, or awesome landscapes adorn the theater of some dramatic Oscar scene. Do you remember Ace Ventura dangling from a rope over that abyss, trying to save the little raccoon? Remember all those beautiful mountains in the background? That was not a location shot. That was computer-generated Chaos art.

Complex systems are systems that contain so much motion (so many elements that move) that computers are required to calculate all the various possibilities. That is why Chaos Theory could not have emerged before the second half of the 20th century.
However, there is another reason that Chaos Theory was born so recently, and that is the ‘Quantum Mechanical Revolution’ and how it ended the ‘deterministic’ era.

Up to the Quantum Mechanical Revolution, people believed that things were directly caused by other things, that what went up had to come down, and that if only we could catch and tag every particle in the universe we could predict events from then on. Entire governments and systems of belief were (and, sadly, are still) founded on these beliefs, and when Sigmund Freud invented psychoanalysis, he headed out from the idea that malfunctions in the mind are the results of traumas suffered in the past. Regression would allow the patient to stroll down memory lane, pinpoint the sore spot and rub it away with Freud's healing techniques that were again based on linear cause and effect.

Chaos Theory however taught us that nature most often works in patterns, which are caused by the sum of many tiny pulses.

How Chaos Theory was born and why

It all started to dawn on people when in 1960 a man named Edward Lorenz [3] created a weather-model on his computer at the Massachusetts Institute of Technology. Lorentz’ weather model consisted of an extensive array of complex formulas that kicked numbers around like an old pigskin. Clouds rose and winds blew, heat scourged or cold came creeping up the breeches.

Colleagues and students marveled over the machine because it never seemed to repeat a sequence; it was really quite like the real weather. Some even hoped that Lorentz had built the ultimate weather-predictor and if one chose the input parameters identical to those of the real weather howling outside the Maclaurin Building, it could mimic earth's atmosphere and would be a precise prophet.

Then one day Lorentz decided to cheat a little bit. A while earlier, he had let the program run on certain parameters to generate a certain weather pattern and he wanted to take a better look at the outcome. Instead of letting the program run from the initial settings and calculate the outcome, Lorentz decided to start half way down the sequence by inputting the values that the computer had come up with during the earlier run.

The computer that Lorentz was working with calculated the various parameters with an accuracy of six decimals; but the printout gave these numbers with a three decimal accuracy. So, instead of inputting certain numbers (like wind, temperature and stuff like that) as accurate as the computer had them, Lorentz settled for approximations; 5.123456 became 5.123 (for instance). And that puny little inaccuracy appeared to amplify and cause the entire system to swing out of whack.

Exactly how important is all this? Well, in the case of weather systems, it is very important. Weather is the total behavior of all the molecules that make up earth's atmosphere; and in the previous chapters, we have established that a tiny particle cannot be accurately pinpointed, due to the Uncertainty Principle! Moreover, this is the sole reason why weather forecasts begin to be bogus around a day or two into the future. We cannot get an accurate fix on the present situation, just a mere approximation, and so our ideas about the weather are doomed to fall into misalignment in a matter of hours, and completely into the nebulas of fantasy within days. Nature will not let herself be predicted.

Principle (7):The Uncertainty Principle prohibits accuracy. Therefore, the initial situation of a complex system cannot be accurately determined, and the evolution of a complex system cannot be accurately predicted.

[1] "It's a Jungle out There" is a song written by Randy Newman, the theme song for the TV series Monk since its second season. In 2004, it won an Emmy Award for best theme song.

[2] Ian Malcolm is played by Jeff Goldblum (please do not tell me you have never heard of him). Jeffrey Lynn "Jeff" Goldblum (born October 22, 1952) is an American actor. His career began in the mid-1970s and since then he has appeared in major box-office successes including The Fly, Jurassic Park (two films), and Independence Day. From 2009 to mid-2010 he starred as Detective Zach Nichols on the USA Network's crime drama series Law & Order: Criminal Intent.

[3] Edward Norton Lorentz (May 23, 1917 - April 16, 2008) was an American mathematician and meteorologist, and a pioneer of chaos theory. He discovered the strange attractor notion and coined the term butterfly effect.

Exerpt from new book: "Quantum Phaith"

"Everyone else would climb a peak by looking for a path somewhere in the mountain. [John] Nash would climb another mountain altogether and from that distant peak would shine a searchlight back onto the first peak."

-Donald Newman (A Beautiful Mind by S. Nasar, p. 12)

Introduction

I have struggled with what should come first, a discussion of biblical faith or a discussion of quantum physics (or quantum mechanics). In the end, I had to consider what came from what. Many scientists would claim that their faith—if they have any at all—evolved from their study of the science. For me it was Biblical faith that revealed the mysteries of mathematics and physics.
There is a verse in Scripture that many know or have heard (even people who have never picked up a Bible). The New American Standard translation of Luke 17:6 says:

And the Lord said, "If you had faith like a mustard seed, you would say to this mulberry tree, ‘Be uprooted and be planted in the sea’; and it would obey you”. (NASB)

I have to admit that my faith is much smaller than mustard seed, which by the way is very tiny. I have always used, not by choice, sweat, blood, and a shovel to move trees (or at least very small trees). Although I have never held a mustard seed, there in an abundance of information about them is available through the internet. I suppose Jesus had first-hand experience when he spoke about a mustard seed—I have no reason to doubt otherwise.

Κόκκος σίναπι (What would we do without mustard seeds?)

The Greek renders Jesus’ reference to a mustard seed as κόκκον σινάπεως, transliterated as kosson sinapeōs. The word Κόκκος, kokkos, is translated five times as ‘grain’ and once as ‘corn’ in the King James Version (KJV). The word σίναπι, sinapi, occurs five times in the KJV and is translated as ‘mustard seed’ in all five instances. Strong’s Lexicon says that mustard is “the name of a plant which in oriental countries grows from a very small seed and attains a height of a tree, 10 feet (3 m) and more; hence a very small quantity of a thing is likened to a mustard seed, and also a thing which grows to a remarkable size.” [Strong, J., The exhaustive concordance of the Bible (electronic ed.). Ontario : Woodside Bible Fellowship, 1996]

The Latin Vulgate renders the verse as:

"dixit autem Dominus si haberetis fidem sicut granum sinapis diceretis huic arbori moro eradicare et transplantare in mare et oboediret vobis"

I mention the Latin here since it is from the Latin word quanta that we derive the English word quantity. I also want to make it clear that the Latin did not render the Greek work for grain as quantum, rather as granum. However, Matthew 13:32 describes the mustard seed as “quod minimum quidem est omnibus seminibus”, that is, “the least indeed of all seeds”. Although I lack direct historical literary evidence that Jesus had in mind the concept of a small quantity when he speaks of a mustard seed, in this case, the context of His words speaks of a “small quantity of a thing”.

Later, we will explore the concept or meaning of biblical faith, but first let’s digress and explore the concept of small quantities of things.

Phundamentals of Physical Quantities

If you are close to my age (52), then you probably remember the television series Quantum Leap. If you are younger, you may have heard terms like quantum computing or quantum numbers. At any rate, you have probably heard the word quantum, whether you paid any attention to it or not.

In physics, a quantum (plural: quanta) is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be ‘quantized’, referred to as ‘the hypothesis of quantization’ [Wiener, N., Differential Space, Quantum Systems, and Prediction. Cambridge : The Massachusetts Institute of Technology Press, 1966]. This means that the magnitude can take on only certain discrete values, leading to the related term called “quantum number”. An example of a quantized entity is the energy transfer of elementary particles of matter (called fermions) and of photons, and other bosons. [Srednicki, Mark., Quantum Field Theory. Cambridge : Cambridge University Press, 2007. ISBN 978-0521864497]

A photon is a single quantum of light, and is referred to as a light quantum. The energy of an electron, bound to an atom (at rest), is said to be quantized, which results in the stability of atoms, and of matter in general. As incorporated into the theory of quantum mechanics, physicists regard this as part of the fundamental framework for understanding and describing nature at the infinitesimal level.

Normally quanta are considered discrete packets with energy stored in them. Max Planck (he won the Nobel Prize for his work in quantum theory) considered these quanta to be particles that can change their form (meaning that they can be absorbed and released). This phenomenon can be observed in the case of blackbody radiation, when it is being heated and cooled.

Phundamentals of Phaith

"Now faith is the assurance of things hoped for, the conviction [evidence] of things not seen."

- Hebrews 11:1 (NASB, brackets added)

"Seeing isn’t believing; believing is seeing."

- The Santa Claus

I have seen the Grand Canyon, walked around the rim, taken photos, and bought something from the myriad of gift shops. It does not take much conviction to assume it is real. Ditto with the Statue of Liberty, Monument Valley, the Saturn V rocket, Disney World, and so on. I did not witness the atomic explosion at Hiroshima (I was not born), the gunfight at the O.K. Corral, the third Crusade, the sack of Jerusalem, or the birth of Christ. However, I have seen historical evidence that all these events occurred, and I do not need conviction to believe they did.

I have not seen (direct) evidence of the eternal life that Christ promised to believers. I’ve heard about it, read about it, watched movies about it, but I have not seen it. I have had parents and in-laws die. They had known Christ in a personal relationship, but I did not see them ascend to heaven. In fact, the last time I saw them was in an urn or in the ground. Yet, I am convicted that they are living eternity with Christ—it is something I have hoped for them and for myself someday. I am assured of this by faith. I stated at the outset (in the preface) that belief is something we get from others, while faith is something we develop for ourselves. That is not entirely accurate. “So faith comes by hearing, and hearing by the word of Christ.” (Romans 10:17, NASB)

So, ‘seeing’ is not involved in developing faith. Rather, it is directly linked to ‘hearing’ the Word of God. Now, I submit to you that the most intellectual people in the world might read the Word of God, and never be moved by it, while a child might hear it—read it with the Spirit speaking to their soul—and have faith.

I am not quite sure I agree precisely with the elf in The Santa Claus, but too often, we look for evidence before we believe. For me, I had to believe before I could see the evidence. It was there right before me for years. I read it, I studied it, and I dissected it. Nevertheless, not until that ‘quantum leap’ of faith came about did I see it. And quantum leap it was—just a tiny little bit, like a mustard seed. I did not have an encounter with death. I did not have any traumatic experience that drove me to faith. In some sense, I just stopped trying to understand on my own. You might call it a Holy Spirit encounter, but I don’t even remember feeling it. One moment it was not there, the next moment it was. I had merely said, “Lord, I give up. I can’t do it on my own.” Voilà, faith arrived. Later we will visit Principle 10c: “Truth can only be noticed when the private perspective is doubted”. There was just too much of me in the way of my understanding. I was looking for conviction in something I could see (the words), but missing the Word that was trying to assure me.

As I recently heard:

“Intimacy with God determines your clarity from God.”

- Pastor Daniel Rolfe [1]

2 Corinthians 4:1-6 says:

"1 Therefore, since through God’s mercy we have this ministry, we do not lose heart. 2 Rather, we have renounced secret and shameful ways; we do not use deception, nor do we distort the word of God. On the contrary, by setting forth the truth plainly we commend ourselves to everyone’s conscience in the sight of God. 3 And even if our gospel is veiled, it is veiled to those who are perishing. 4 The god of this age has blinded the minds of unbelievers, so that they cannot see the light of the gospel that displays the glory of Christ, who is the image of God. 5 For what we preach is not ourselves, but Jesus Christ as Lord, and ourselves as your servants for Jesus’ sake. 6 For God, who said, “Let light shine out of darkness,” made his light shine in our hearts to give us the light of the knowledge of God’s glory displayed in the face of Christ. (NIV)

Well now, if God’s Word—Christ—is not believable to you, then you have no hope in understanding it, no matter how educated you have become. If His word is not clear to you, then perhaps you are not intimate enough with Him!"

[1] Daniel Rolfe is a senior pastor at Mountain Springs Church in Colorado Springs, CO.

http://www.lulu.com/product/hardcover/quantum-phaith/16231128