Forest Gump and the Normal Distribution

"I may not be a smart man, but I know what love is." Forrest is a fictional character and was deemed by the experts as having a well below average IQ; however as far as fiction goes, I think he was a lot more intelligent than Jenny. Maybe he listened to his Mama. Psychologist Alfred Binet, said:


"It seems to us that in intelligence there is a fundamental faculty, the alteration or the lack of which, is of the utmost importance for practical life. This faculty is judgment, otherwise called good sense, practical sense, initiative, the faculty of adapting one's self to circumstances. A person may be a moron or an imbecile if he is lacking in judgment; but with good judgment he can never be either. Indeed the rest of the intellectual faculties seem of little importance in comparison with judgment" (Binet & Simon, 1916, 1973, pp.42-43).


So, what does Forrest have to do with the normal distribution? IQ scores are said to follow a bell-shaped curve, or normal distribution. Technically, the normal distribution does not really work, because there is a chance that a test score could be negative, unless you truncate (fix the distribution so as not to allow negative scores). However, the normal distribution works well in describing the distribution of standardized test scores, for example IQ, SAT, etc.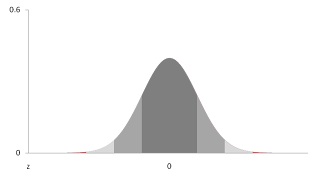



A Little History

The Stanford Binet Scale is widely known for measuring intelligence levels of individuals between the ages of 2 to 85+ years. This test was the result of the revision by Lewis Terman in 1916 to the Binet-Simon Scale. Since 1916 there have been many revisions to the test. It was the first published intelligence test to supply detailed administration and scoring procedures was the first American test to use the idea of the intelligence quotient (IQ). (Laurent, Swerdlik, & Ryburn, 1992.) Currently, it is in its Fifth Edition. The Stanford-Binet metric is based on an average or mean score of 100.

Importance of the Normal Distribution

The term "normal" possibly arose because of the various attempts made to establish this distribution as the underlying rule governing all continuous variables. These attempts were based on false premises and consequently failed. Nonetheless, the normal distribution rightly occupies a preeminent place in the field of probability. In addition to portraying the distribution of many types of natural and physical phenomena (such as the heights of men, diameters of machined parts, etc.), it also serves as a convenient approximation of many other distributions which are less tractable. Most importantly, it describes the manner in which certain estimators of population characteristics vary from sample to sample and, thereby, serves as the foundation upon which much statistical inference from a random sample to population are made.

About 68% of values drawn from a normal distribution are within one standard deviation σ > 0 away from the mean μ; about 95% of the values are within two standard deviations and about 99.7% lie within three standard deviations. This is known as the 68-95-99.7 rule, or the empirical rule, or the 3-sigma rule.




IQ Scores and the Normal Distribution


IQ Scores are said to follow a normal distribution with a mean of 100 and a standard deviation of 10 (approximately). Thus, if you have a IQ score between 90 and 110, you are within 0ne standard deviation of the mean. (If you have taken any standardized test, you have probably seen or heard these terms before.) About 15% of the population have scores greater than 110 or less that 90. Approximately 2% of the population have IQ scores above 120 or below 80. Less than 1% have scores greater than 130 or less than 70.


Now, I am not saying that I agree with IQ scores. If we take fictional Forrest as a representative of some actual person, and apply Alfred Binet's definition of intelligence, IQ scores may not tell the whole story about intelligence.

Incidentally, What was Forrest Gump's IQ score?