In my next series of articles, I will demonstrate how to use the R statistical software to carry out some simple multivariate analyses, with a focus on principal components analysis (PCA) and linear discriminant analysis (LDA). PCA and LDA, will constitute parts II and III, respectively.
The first thing that you will want to do to analyze your multivariate data will be to load it into R, and to plot the data. You can load dataset into R using the require(rattle), ‘wine’ is a data set in this package. The dataset ‘wine’ contains data on concentrations of 13 different chemicals in wines grown in the same region in Italy that are derived from three different cultivars.
There is one row per wine sample. The first column contains the cultivar of a wine sample (labelled 1, 2 or 3), and the following thirteen columns contain the concentrations of the 13 different chemicals in that sample. The columns are separated by commas. We can load in the file using the require() function as follows:
require(rattle)wine # a dataset in the rattle package
V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14
1 1 14.23 1.71 2.43 15.6 127 2.80 3.06 0.28 2.29 5.640000 1.040 3.92 1065
2 1 13.20 1.78 2.14 11.2 100 2.65 2.76 0.26 1.28 4.380000 1.050 3.40 1050
3 1 13.16 2.36 2.67 18.6 101 2.80 3.24 0.30 2.81 5.680000 1.030 3.17 1185
4 1 14.37 1.95 2.50 16.8 113 3.85 3.49 0.24 2.18 7.800000 0.860 3.45 1480
5 1 13.24 2.59 2.87 21.0 118 2.80 2.69 0.39 1.82 4.320000 1.040 2.93 735
...
176 3 13.27 4.28 2.26 20.0 120 1.59 0.69 0.43 1.35 10.200000 0.590 1.56 835
177 3 13.17 2.59 2.37 20.0 120 1.65 0.68 0.53 1.46 9.300000 0.600 1.62 840
178 3 14.13 4.10 2.74 24.5 96 2.05 0.76 0.56 1.35 9.200000 0.610 1.60 560In this case the data on 178 samples of wine has been read into the variable ‘wine’.
Plotting Multivariate Data
Once you have read a multivariate data set into R, the next step is usually to make a plot of the data.A Matrix Scatterplot
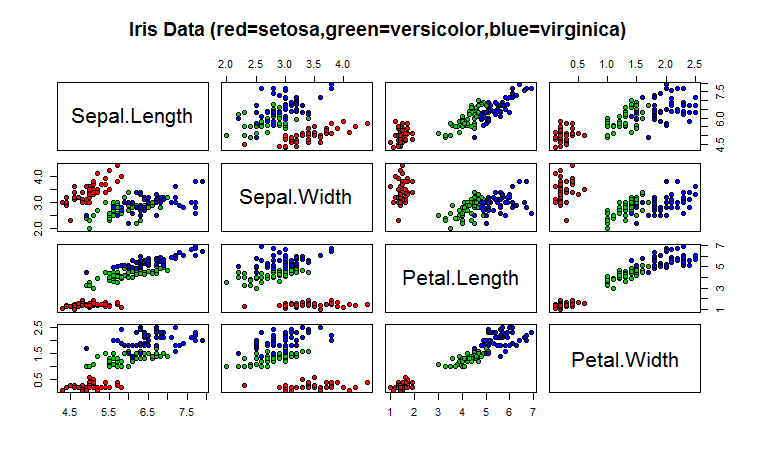
One common way of plotting multivariate data is to make a “matrix scatterplot”, showing each pair of variables plotted against each other. We can use the “scatterplotMatrix()” function from the “car” R package to do this. To use this function, we first need to install the “car” R package (for instructions on how to install an R package, see How to install an R package).
Once you have installed the “car” R package, you can load the “car” R package by typing:
> library("car")You can then use the “scatterplotMatrix()” function to plot the multivariate data.
To use the scatterplotMatrix() function, you need to give it as its input the variables that you want included in the plot. Say for example, that we just want to include the variables corresponding to the concentrations of the first five chemicals. These are stored in columns 2-6 of the variable “wine”. We can extract just these columns from the variable “wine” by typing:
> wine[2:6]
V2 V3 V4 V5 V6
1 14.23 1.71 2.43 15.6 127
2 13.20 1.78 2.14 11.2 100
3 13.16 2.36 2.67 18.6 101
4 14.37 1.95 2.50 16.8 113
5 13.24 2.59 2.87 21.0 118
...To make a matrix scatterplot of just these 13 variables using the scatterplotMatrix() function we type:
> scatterplotMatrix(wine[2:6])
Each of the off-diagonal cells is a scatterplot of two of the five chemicals, for example, the second cell in the first row is a scatterplot of V2 (y-axis) against V3 (x-axis).
A Scatterplot with the Data Points Labelled by their Group
If you see an interesting scatterplot for two variables in the matrix scatterplot, you may want to plot that scatterplot in more detail, with the data points labelled by their group (their cultivar in this case).
For example, in the matrix scatterplot above, the cell in the third column of the fourth row down is a scatterplot of V5 (x-axis) against V4 (y-axis). If you look at this scatterplot, it appears that there may be a positive relationship between V5 and V4.
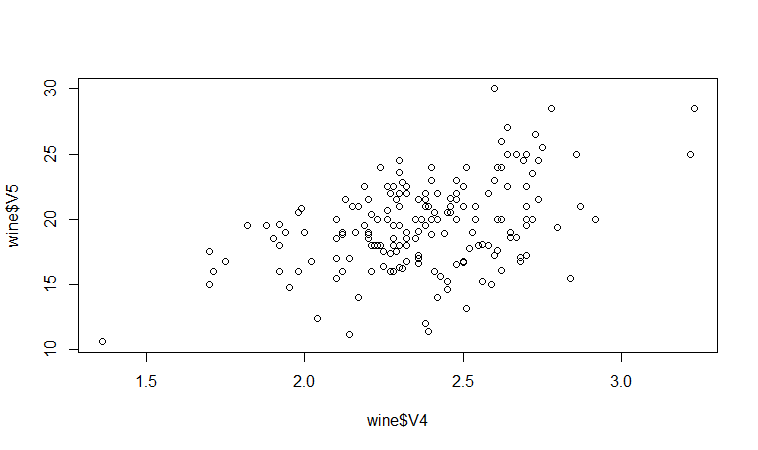
We may therefore decide to examine the relationship between V5 and V4 more closely, by plotting a scatterplot of these two variable, with the data points labelled by their group (their cultivar). To plot a scatterplot of two variables, we can use the “plot” R function. The V4 and V5 variables are stored in the columns V4 and V5 of the variable “wine”, so can be accessed by typing wine$V4 or wine$V5. Therefore, to plot the scatterplot, we type:
> plot(wine$V4, wine$V5)
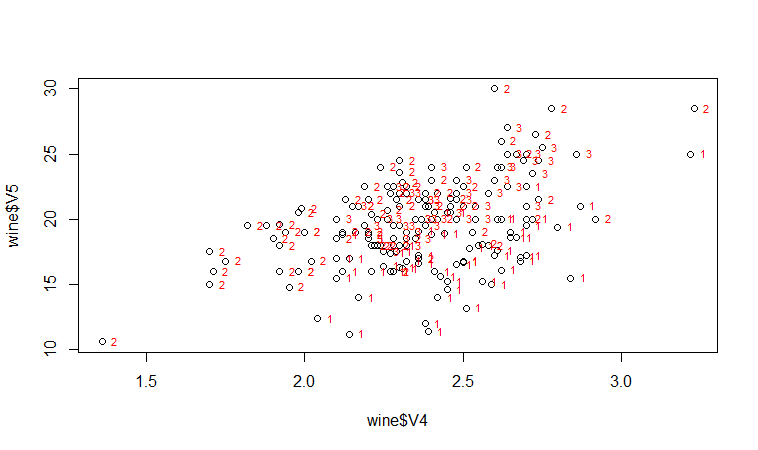
If we want to label the data points by their group (the cultivar of wine here), we can use the “text” function in R to plot some text beside every data point. In this case, the cultivar of wine is stored in the column V1 of the variable “wine”, so we type:
> text(wine$V4, wine$V5, wine$V1, cex=0.7, pos=4, col="red")
If you look at the help page for the “text” function, you will see that “pos=4” will plot the text just to the right of the symbol for a data point. The “cex=0.5” option will plot the text at half the default size, and the “col=red” option will plot the text in red. This gives us the following plot:
We can see from the scatterplot of V4 versus V5 that the wines from cultivar 2 seem to have lower values of V4 compared to the wines of cultivar 1.
A Profile Plot
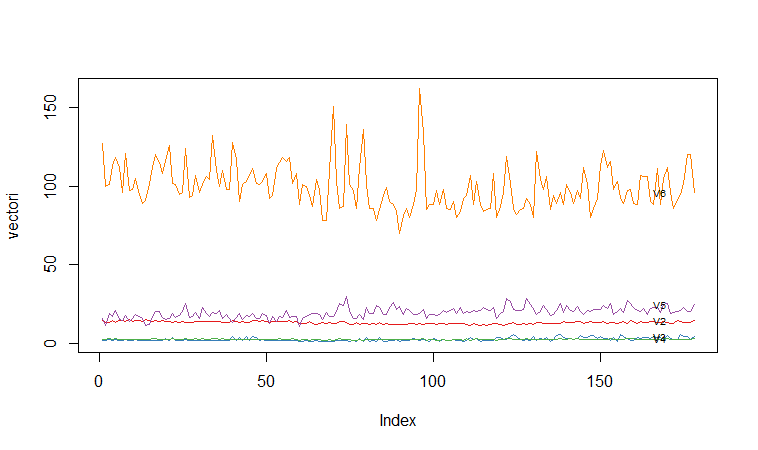
Another type of plot that is useful is a “profile plot”, which shows the variation in each of the variables, by plotting the value of each of the variables for each of the samples.The function “makeProfilePlot()” below can be used to make a profile plot. This function requires the “RColorBrewer” library. To use this function, we first need to install the “RColorBrewer” R package (for instructions on how to install an R package, see How to install an R package).
> makeProfilePlot {
require(RColorBrewer)
# find out how many variables we want to include numvariables # choose 'numvariables' random colours
colours # find out the minimum and maximum values of the variables: mymin mymax for (i in 1:numvariables)
{
vectori mini maxi if (mini < mymin) { mymin mymax) { mymax }
# plot the variables
for (i in 1:numvariables)
{
vectori namei colouri if (i == 1) { plot(vectori,col=colouri,type="l",ylim=c(mymin,mymax)) }
else { points(vectori, col=colouri,type="l") }
lastxval lastyval text((lastxval-10),(lastyval),namei,col="black",cex=0.6)
}
}To use this function, you first need to copy and paste it into R. The arguments to the function are a vector containing the names of the varibles that you want to plot, and a list variable containing the variables themselves.
For example, to make a profile plot of the concentrations of the first five chemicals in the wine samples (stored in columns V2, V3, V4, V5, V6 of variable “wine”), we type:
> library(RColorBrewer)
> names mylist makeProfilePlot(mylist,names)
It is clear from the profile plot that the mean and standard deviation for V6 is quite a lot higher than that for the other variables.
Calculating Summary Statistics for Multivariate Data
Another thing that you are likely to want to do is to calculate summary statistics such as the mean and standard deviation for each of the variables in your multivariate data set.
sapply
The “sapply()” function can be used to apply some other function to each column in a data frame, eg. sapply(mydataframe,sd) will calculate the standard deviation of each column in a dataframe “mydataframe”.
This is easy to do, using the “mean()” and “sd()” functions in R. For example, say we want to calculate the mean and standard deviations of each of the 13 chemical concentrations in the wine samples. These are stored in columns 2-14 of the variable “wine”. So we type:
> sapply(wine[2:14],mean)
V2 V3 V4 V5 V6 V7
13.0006180 2.3363483 2.3665169 19.4949438 99.7415730 2.2951124
V8 V9 V10 V11 V12 V13
2.0292697 0.3618539 1.5908989 5.0580899 0.9574494 2.6116854
V14
746.8932584This tells us that the mean of variable V2 is 13.0006180, the mean of V3 is 2.3363483, and so on.
Similarly, to get the standard deviations of the 13 chemical concentrations, we type:
> sapply(wine[2:14],sd)
V2 V3 V4 V5 V6 V7
0.8118265 1.1171461 0.2743440 3.3395638 14.2824835 0.6258510
V8 V9 V10 V11 V12 V13
0.9988587 0.1244533 0.5723589 2.3182859 0.2285716 0.7099904
V14
314.9074743We can see here that it would make sense to standardize in order to compare the variables because the variables have very different standard deviations – the standard deviation of V14 is 314.9074743, while the standard deviation of V9 is just 0.1244533. Thus, in order to compare the variables, we need to standardize each variable so that it has a sample variance of 1 and sample mean of 0. We will explain below how to standardize the variables.
Means and Variances Per Group
It is often interesting to calculate the means and standard deviations for just the samples from a particular group, for example, for the wine samples from each cultivar. The cultivar is stored in the column “V1” of the variable “wine”.
> cultivar2wine We can then calculate the mean and standard deviations of the 13 chemicals’ concentrations, for just the cultivar 2 samples:
sapply(cultivar2wine[2:14],mean)
V2 V3 V4 V5 V6 V7 V8
12.278732 1.932676 2.244789 20.238028 94.549296 2.258873 2.080845
V9 V10 V11 V12 V13 V14
0.363662 1.630282 3.086620 1.056282 2.785352 519.507042
> sapply(cultivar2wine[2:14])
V2 V3 V4 V5 V6 V7 V8
0.5379642 1.0155687 0.3154673 3.3497704 16.7534975 0.5453611 0.7057008
V9 V10 V11 V12 V13 V14
0.1239613 0.6020678 0.9249293 0.2029368 0.4965735 157.2112204You can calculate the mean and standard deviation of the 13 chemicals’ concentrations for just cultivar 1 samples, or for just cultivar 3 samples, in a similar way.
However, for convenience, you might want to use the function “printMeanAndSdByGroup()” below, which prints out the mean and standard deviation of the variables for each group in your data set:
> printMeanAndSdByGroup function(variables,groupvariable)
{
# find the names of the variables
variablenames # within each group, find the mean of each variable
groupvariable # ensures groupvariable is not a list
means names(means) print(paste("Means:"))
print(means)
# within each group, find the standard deviation of each variable:
sds names(sds) print(paste("Standard deviations:"))
print(sds)
# within each group, find the number of samples:
samplesizes names(samplesizes) print(paste("Sample sizes:"))
print(samplesizes)
}To use the function “printMeanAndSdByGroup()”, you first need to copy and paste it into R. The arguments of the function are the variables that you want to calculate means and standard deviations for, and the variable containing the group of each sample. For example, to calculate the mean and standard deviation for each of the 13 chemical concentrations, for each of the three different wine cultivars, we type:
> printMeanAndSdByGroup(wine[2:14],wine[1])
[1] "Means:"
V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14
1 1 13.7448 2.0107 2.4556 17.0370 106.3390 2.8402 2.9824 0.2900 1.8993 5.5283 1.0620 3.1578 1115.7119
2 2 12.2787 1.9327 2.2448 20.2380 94.5493 2.2589 2.0808 0.3637 1.6303 3.0866 1.0563 2.7854 519.5070
3 3 13.1536 3.3338 2.4371 21.4167 99.3125 1.6788 0.7815 0.4475 1.1535 7.3963 0.6827 1.6835 629.8958
[1] "Standard deviations:" V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14
1 1 0.4621 0.6885 0.2272 2.5463 10.4990 0.3390 0.3975 0.0701 0.4121 1.2386 0.1164 0.3571 221.5208
2 2 0.5380 1.0156 0.3155 3.3498 16.7535 0.5454 0.7057 0.1240 0.6021 0.9250 0.2029 0.4966 157.2112
3 3 0.5302 1.0879 0.1846 2.2582 10.8905 0.3570 0.2935 0.1241 0.4088 2.3101 0.1144 0.2721 115.0970[1] "Sample sizes:"
V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14
1 1 59 59 59 59 59 59 59 59 59 59 59 59 59
2 2 71 71 71 71 71 71 71 71 71 71 71 71 71
3 3 48 48 48 48 48 48 48 48 48 48 48 48 48The function “printMeanAndSdByGroup()” also prints out the number of samples in each group. In this case, we see that there are 59 samples of cultivar 1, 71 of cultivar 2, and 48 of cultivar 3.
Between-groups Variance and Within-groups Variance for a Variable
If we want to calculate the within-groups variance for a particular variable (for example, for a particular chemical’s concentration), we can use the function “calcWithinGroupsVariance()” below:
> calcWithinGroupsVariance function(variable,groupvariable){
# find out how many values the group variable can take
groupvariable2 levels numlevels # get the mean and standard deviation for each group:
numtotal denomtotal for (i in 1:numlevels)
{
leveli levelidata levelilength # get the standard deviation for group i: sdi numi denomi numtotal denomtotal }
# calculate the within-groups variance
Vw return(Vw)
}You will need to copy and paste this function into R before you can use it. For example, to calculate the within-groups variance of the variable V2 (the concentration of the first chemical), we type:
> calcWithinGroupsVariance(wine[2],wine[1])
[1] 0.2620525Thus, the within-groups variance for V2 is 0.2620525.
We can calculate the between-groups variance for a particular variable (eg. V2) using the function “calcBetweenGroupsVariance()” below:
> calcBetweenGroupsVariance function(variable,groupvariable){
# find out how many values the group variable can take groupvariable2 levels numlevels # calculate the overall grand mean: grandmean # get the mean and standard deviation for each group: numtotal denomtotal for (i in 1:numlevels)
{
leveli levelidata levelilength # get the mean and standard deviation for group i:
meani sdi numi denomi numtotal denomtotal }
# calculate the between-groups variance Vb Vb return(Vb)
}
Once you have copied and pasted this function into R, you can use it to calculate the between-groups variance for a variable such as V2:
> calcBetweenGroupsVariance (wine[2],wine[1])
[1] 35.39742Thus, the between-groups variance of V2 is 35.39742.
We can calculate the “separation” achieved by a variable as its between-groups variance divided by its within-groups variance. Thus, the separation achieved by V2 is calculated as:
> 35.39742/0.2620525
[1] 135.0776If you want to calculate the separations achieved by all of the variables in a multivariate data set, you can use the function “calcSeparations()” below:
> calcSeparations function(variables,groupvariable){
# find out how many variables we have variables numvariables # find the variable names variablenames # calculate the separation for each variable for (i in 1:numvariables)
{
variablei variablename Vw Vb sep print(paste("variable",variablename,"Vw=",Vw,"Vb=",Vb,"separation=",sep))
}
}For example, to calculate the separations for each of the 13 chemical concentrations, we type:
> calcSeparations(wine[2:14],wine[1])
[1] "variable V2 Vw= 0.2620524692 Vb= 35.39742496027 separation= 135.07762424"
[1] "variable V3 Vw= 0.8875467967 Vb= 32.78901848692 separation= 36.943424963"
[1] "variable V4 Vw= 0.0660721013 Vb= 0.879611357249 separation= 13.312901199"
[1] "variable V5 Vw= 8.0068111812 Vb= 286.4167463631 separation= 35.771637407"
[1] "variable V6 Vw= 180.65777316 Vb= 2245.501027890 separation= 12.429584338"
[1] "variable V7 Vw= 0.1912704752 Vb= 17.92835729429 separation= 93.733009620"
[1] "variable V8 Vw= 0.2747075143 Vb= 64.26119502356 separation= 233.92587268"
[1] "variable V9 Vw= 0.0119117022 Vb= 0.328470157461 separation= 27.575417146"
[1] "variable V10 Vw= 0.2461729438 Vb= 7.451995507778 separation= 30.271383170"
[1] "variable V11 Vw= 2.2849230813 Vb= 275.7080008223 separation= 120.66401844"
[1] "variable V12 Vw= 0.0244876469 Vb= 2.481009914938 separation= 101.31679539"
[1] "variable V13 Vw= 0.1607787296 Vb= 30.54350835443 separation= 189.97232058"
[1] "variable V14 Vw= 29707.681871 Vb= 6176832.322285 separation= 207.92037390"Thus, the individual variable which gives the greatest separations between the groups (the wine cultivars) is V8 (separation 233.9). As we will discuss below, the purpose of linear discriminant analysis (LDA) is to find the linear combination of the individual variables that will give the greatest separation between the groups (cultivars here). This hopefully will give a better separation than the best separation achievable by any individual variable (233.9 for V8 here).
Between-groups Covariance and Within-groups Covariance for Two Variables
If you have a multivariate data set with several variables describing sampling units from different groups, such as the wine samples from different cultivars, it is often of interest to calculate the within-groups covariance and between-groups variance for pairs of the variables.
This can be done using the following functions, which you will need to copy and paste into R to use them:
> calcWithinGroupsCovariance function(variable1,variable2,groupvariable){
# find out how many values the group variable can take
groupvariable2 levels numlevels # get the covariance of variable 1 and variable 2 for each group:
Covw for (i in 1:numlevels)
{
leveli levelidata1 levelidata2 mean1 mean2 levelilength # get the covariance for this group:
term1 for (j 1:levelilength)
{
term1 }
Cov_groupi # covariance for this group
Covw }
totallength Covw return(Covw)
}For example, to calculate the within-groups covariance for variables V8 and V11, we type:
> calcWithinGroupsCovariance(wine[8],wine[11],wine[1])
[1] 0.2866783> calcBetweenGroupsCovariance function(variable1,variable2,groupvariable)
{
# find out how many values the group variable can take
groupvariable2 levels numlevels # calculate the grand means
variable1mean variable2mean # calculate the between-groups covariance
Covb for (i in 1:numlevels)
{
leveli levelidata1 levelidata2 mean1 mean2 levelilength term1 Covb }
Covb Covb return(Covb)
}For example, to calculate the between-groups covariance for variables V8 and V11, we type:
> calcBetweenGroupsCovariance(wine[8],wine[11],wine[1])
[1] -60.41077Thus, for V8 and V11, the between-groups covariance is -60.41 and the within-groups covariance is 0.29. Since the within-groups covariance is positive (0.29), it means V8 and V11 are positively related within groups: for individuals from the same group, individuals with a high value of V8 tend to have a high value of V11, and vice versa. Since the between-groups covariance is negative (-60.41), V8 and V11 are negatively related between groups: groups with a high mean value of V8 tend to have a low mean value of V11, and vice versa.
Calculating Correlations for Multivariate Data
It is often of interest to investigate whether any of the variables in a multivariate data set are significantly correlated.
To calculate the linear (Pearson) correlation coefficient for a pair of variables, you can use the “cor.test()” function in R. For example, to calculate the correlation coefficient for the first two chemicals’ concentrations, V2 and V3, we type:
> cor.test(wine$V2, wine$V3) Pearson's product-moment correlation
data: wine$V2 and wine$V3
t = 1.2579, df = 176, p-value = 0.2101
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.05342959 0.23817474
sample estimates:
cor
0.09439694This tells us that the correlation coefficient is about 0.094, which is a very weak correlation. Furthermore, the P-value for the statistical test of whether the correlation coefficient is significantly different from zero is 0.21. This is much greater than 0.05 (which we can use here as a cutoff for statistical significance), so there is very weak evidence that that the correlation is non-zero.
If you have a lot of variables, you can use “cor.test()” to calculate the correlation coefficient for each pair of variables, but you might be just interested in finding out what are the most highly correlated pairs of variables. For this you can use the function “mosthighlycorrelated()” below.
The function “mosthighlycorrelated()” will print out the linear correlation coefficients for each pair of variables in your data set, in order of the correlation coefficient. This lets you see very easily which pair of variables are most highly correlated.
> mosthighlycorrelated function(mydataframe,numtoreport)
{
# find the correlations
cormatrix # set the correlations on the diagonal or lower triangle to zero,
# so they will not be reported as the highest ones:
diag(cormatrix) cormatrix[lower.tri(cormatrix)] # flatten the matrix into a dataframe for easy sorting
fm # assign human-friendly names
names(fm) # sort and print the top n correlations
head(fm[order(abs(fm$Correlation),decreasing=T),],n=numtoreport)
}To use this function, you will first have to copy and paste it into R. The arguments of the function are the variables that you want to calculate the correlations for, and the number of top correlation coefficients to print out (for example, you can tell it to print out the largest ten correlation coefficients, or the largest 20).
For example, to calculate correlation coefficients between the concentrations of the 13 chemicals in the wine samples, and to print out the top 10 pairwise correlation coefficients, you can type:
> mosthighlycorrelated(wine[2:14], 10)
First.Variable Second.Variable Correlation
84 V7 V8 0.8645635
150 V8 V13 0.7871939
149 V7 V13 0.6999494
111 V8 V10 0.6526918
157 V2 V14 0.6437200
110 V7 V10 0.6124131
154 V12 V13 0.5654683
132 V3 V12 -0.5612957
118 V2 V11 0.5463642
137 V8 V12 0.5434786This tells us that the pair of variables with the highest linear correlation coefficient are V7 and V8 (correlation = 0.86 approximately).
Standardizing Variables
If you want to compare different variables that have different units, are very different variances, it is a good idea to first standardize the variables.
For example, we found above that the concentrations of the 13 chemicals in the wine samples show a wide range of standard deviations, from 0.1244533 for V9 (variance 0.01548862) to 314.9074743 for V14 (variance 99166.72). This is a range of approximately 6,402,554-fold in the variances.
As a result, it is not a good idea to use the unstandardized chemical concentrations as the input for a principal component analysis (PCA, see below) of the wine samples, as if you did that, the first principal component would be dominated by the variables which show the largest variances, such as V14.
Thus, it would be a better idea to first standardize the variables so that they all have variance 1 and mean 0, and to then carry out the principal component analysis on the standardized data. This would allow us to find the principal components that provide the best low-dimensional representation of the variation in the original data, without being overly biased by those variables that show the most variance in the original data.
You can standardize variables in R using the “scale()” function.
For example, to standardize the concentrations of the 13 chemicals in the wine samples, we type:
> standardizedconcentrations Note that we use the “as.data.frame()” function to convert the output of “scale()” into a “data frame”, which is the same type of R variable that the “wine” variable.
We can check that each of the standardized variables stored in “standardizedconcentrations” has a mean of 0 and a standard deviation of 1 by typing:
> sapply(standardizedconcentrations,mean)
V2 V3 V4 V5 V6 V7
-8.591766e-16 -6.776446e-17 8.045176e-16 -7.720494e-17 -4.073935e-17 -1.395560e-17
V8 V9 V10 V11 V12 V13
6.958263e-17 -1.042186e-16 -1.221369e-16 3.649376e-17 2.093741e-16 3.003459e-16
V14
-1.034429e-16
> sapply(standardizedconcentrations,sd)
V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14
1 1 1 1 1 1 1 1 1 1 1 1 1
We see that the means of the standardized variables are all very tiny numbers and so are essentially equal to 0, and the standard deviations of the standardized variables are all equal to 1.
Authored by: Jeffrey Strickland, Ph.D.
Jeffrey Strickland, Ph.D., is the Author of “Predictive Analytics Using R” and a Senior Analytics Scientist with Clarity Solution Group. He has performed predictive modeling, simulation and analysis for the Department of Defense, NASA, the Missile Defense Agency, and the Financial and Insurance Industries for over 20 years. Jeff is a Certified Modeling and Simulation professional (CMSP) and an Associate Systems Engineering Professional. He has published nearly 200 blogs on LinkedIn, is also a frequently invited guest speaker and the author of 20 books including:
- Operations Research using Open-Source Tools
- Discrete Event simulation using ExtendSim
- Crime Analysis and Mapping
- Missile Flight Simulation
- Mathematical Modeling of Warfare and Combat Phenomenon
- Predictive Modeling and Analytics
- Using Math to Defeat the Enemy
- Verification and Validation for Modeling and Simulation
- Simulation Conceptual Modeling
- System Engineering Process and Practices
- Weird Scientist: the Creators of Quantum Physics
- Albert Einstein: No one expected me to lay a golden eggs
- The Men of Manhattan: the Creators of the Nuclear Era
- Fundamentals of Combat Modeling
- LinkedIn Memoirs
- Quantum Phaith
- Dear Mister President
- Handbook of Handguns
- Knights of the Cross: The True Story of the Knights Templar