What is Time-Series Analysis, Part 2?

 

This article first appeared on bicorner.com

In my last article I talked about Time Series Analysis using R and left with simple exponential smoothing. Here I want to talk about more advanced smoothing methods.

Holt’s Exponential Smoothing

If you have a time series that can be described using an additive model with increasing or decreasing trend and no seasonality, you can use Holt’s exponential smoothing to make short-term forecasts.

 

Holt’s exponential smoothing estimates the level and slope at the current time point. Smoothing is controlled by two parameters, alpha, for the estimate of the level at the current time point, and beta for the estimate of the slope b of the trend component at the current time point. As with simple exponential smoothing, the parameters alpha and beta have values between 0 and 1, and values that are close to 0 mean that little weight is placed on the most recent observations when making forecasts of future values.

 

ADVERTISEMENT

An example of a time series that can probably be described using an additive model with a trend and no seasonality is the time series of US Treasury bill contracts on the Chicago market for 100 consecutive trading days in 1981.

 

We can read in and plot the data in R by typing:

 

> install.packages("fma")
> ustreasseries > plot.ts(ustreasseries)

 

 

To make forecasts, we can fit a predictive model using the HoltWinters() function in R. To use HoltWinters() for Holt’s exponential smoothing, we need to set the parameter gamma=FALSE (the gamma parameter is used for Holt-Winters exponential smoothing, as described below).

 

For example, to use Holt’s exponential smoothing to fit a predictive model for US Treasury bill contracts, we type:

 

> ustreasseriesforecasts ustreasseriesforecasts
Holt-Winters exponential smoothing with trend and without seasonal component.
Call:
HoltWinters(x = ustreasseries, gamma = FALSE) Smoothing parameters:
alpha:
1 beta : 0.01073
gamma: FALSE
Coefficients:
[,1]
a 85.32000000
b -0.04692665
> ustreasseriesforecasts$SSE
[1] 8.707433

 

The estimated value of alpha is 1.0, and of beta is 0.0107. These are both high, telling us that both the estimate of the current value of the level, and of the slope b of the trend component, are based mostly upon very recent observations in the time series. This makes good intuitive sense, since the level and the slope of the time series both change quite a lot over time. The value of the sum-of-squared-errors for the in-sample forecast errors is 8.707.

 

We can plot the original time series as a black line, with the forecasted values as a red line on top of that, by typing:

 

> plot(ustreasseriesforecasts)

 

 

 

We can see from the picture that the in-sample forecasts agree pretty well with the observed values, although they tend to lag behind the observed values a little bit.

 

If you wish, you can specify the initial values of the level and the slope b of the trend component by using the “l.start” and “b.start” arguments for the HoltWinters() function. It is common to set the initial value of the level to the first value in the time series (92 for the Chicago market data), and the initial value of the slope to the second value minus the first value (0.1 for the Chicago market data). For example, to fit a predictive model to the Chicago market data using Holt’s exponential smoothing, with initial values of 608 for the level and 0.1 for the slope b of the trend component, we type:

 

> HoltWinters(ustreasseries, gamma=FALSE, l.start=92, b.start=0.1)
Holt-Winters exponential smoothing with trend and without seasonal component.
Call:
HoltWinters(x = ustreasseries, gamma = FALSE, l.start = 92, b.start = 0.1)
Smoothing parameters:
alpha: 1
beta : 0.04529601
gamma: FALSE
Coefficients:
[,1]
a 85.32000000
b -0.08157293
> ustreasseriesforecasts$SSE
[1] 8.707433

As for simple exponential smoothing, we can make forecasts for future times not covered by the original time series by using the forecast.HoltWinters() function in the “forecast” package. For example, our time series data for the Chicago market was for 0 to 100 days, so we can make predictions for 101-120 (20 more data points), and plot them, by typing:

 

> ustreasseriesforecasts2> plot.forecast(ustreasseriesforecasts2)

 

 

The forecasts are shown as a blue line, with the 80% prediction intervals as an gray shaded area, and the 95% prediction intervals as a light gray shaded area.

 

As for simple exponential smoothing, we can check whether the predictive model could be improved upon by checking whether the in-sample forecast errors show non-zero autocorrelations at lags 1-20. For example, for the Chicago market data, we can make a correlogram, and carry out the Ljung-Box test, by typing:

 

> acf(ustreasseriesforecasts2$residuals, lag.max=20)> Box.test(ustreasseriesforecasts2$residuals, lag=30, type="Ljung-Box")
Box-Ljung test
data:  ustreasseriesforecasts2$residuals
X-squared = 30.4227, df = 30, p-value = 0.4442

 

 

Here the correlogram shows that the sample autocorrelation for the in-sample forecast errors at lag 15 exceeds the significance bounds. However, we would expect one in 20 of the autocorrelations for the first twenty lags to exceed the 95% significance bounds by chance alone. Indeed, when we carry out the Ljung-Box test, the p-value is 0.4442, indicating that there is little evidence of non-zero autocorrelations in the in-sample forecast errors at lags 1-20.

 

As for simple exponential smoothing, we should also check that the forecast errors have constant variance over time, and are normally distributed with mean zero. We can do this by making a time plot of forecast errors, and a histogram of the distribution of forecast errors with an overlaid normal curve:

 

> plot.ts(ustreasseriesforecasts2$residuals)           # make a time plot
> plotForecastErrors(ustreasseriesforecasts2$residuals) # make a histogram

 

 

The time plot of forecast errors shows that the forecast errors have roughly constant variance over time. The histogram of forecast errors show that it is plausible that the forecast errors are normally distributed with mean zero and constant variance.

 

Thus, the Ljung-Box test shows that there is little evidence of autocorrelations in the forecast errors, while the time plot and histogram of forecast errors show that it is plausible that the forecast errors are normally distributed with mean zero and constant variance. Therefore, we can conclude that Holt’s exponential smoothing provides an adequate predictive model for the US Treasury bill contracts on the Chicago market, which probably cannot be improved upon. In addition, it means that the assumptions that the 80% and 95% predictions intervals were based upon are probably valid.

Holt-Winters Exponential Smoothing

If you have a time series that can be described using an additive model with increasing or decreasing trend and seasonality, you can use Holt-Winters exponential smoothing to make short-term forecasts.

 

Holt-Winters exponential smoothing estimates the level, slope and seasonal component at the current time point. Smoothing is controlled by three parameters: alpha, beta, and gamma, for the estimates of the level, slope b of the trend component, and the seasonal component, respectively, at the current time point. The parameters alpha, beta and gamma all have values between 0 and 1, and values that are close to 0 mean that relatively little weight is placed on the most recent observations when making forecasts of future values.

 

An example of a time series that can probably be described using an additive model with a trend and seasonality is the time series of the US Birth data we have already used (discussed in previous article: “What is Time Series Analysis?)

 

> birthtimeseriesforecasts birthtimeseriesforecasts
Holt-Winters exponential smoothing with trend and additive seasonal component.
Call:
HoltWinters(x = birthtimeseries) Smoothing
parameters:
alpha: 0.5388189
beta : 0.005806264
gamma: 0.1674998
Coefficients:
[,1]
a   279.37339259
b    -0.07077833
s1  -24.22000167
s2   -1.13886091
s3  -19.75018141
s4  -10.15418869
s5  -12.58375567
s6   11.96501002
s7   20.74652186
s8   18.21566037
s9   12.93338079
s10  -4.86769013
s11   4.49894836
s12 -4.59412722
> birthtimeseriesforecasts$SSE
[1] 19571.77

The estimated values of alpha, beta and gamma are 0.5388, 0.0058, and 0.1675, respectively. The value of alpha (0.5388) is relatively low, indicating that the estimate of the level at the current time point is based upon both recent observations and some observations in the more distant past. The value of beta is 0.0058, indicating that the estimate of the slope b of the trend component is not updated over the time series, and instead is set equal to its initial value. This makes good intuitive sense, as the level changes quite a bit over the time series, but the slope b of the trend component remains roughly the same. In contrast, the value of gamma (0.1675) is low, indicating that the estimate of the seasonal component at the current time point is based upon less recent observations.

 

As for simple exponential smoothing and Holt’s exponential smoothing, we can plot the original time series as a black line, with the forecasted values as a red line on top of that:

 

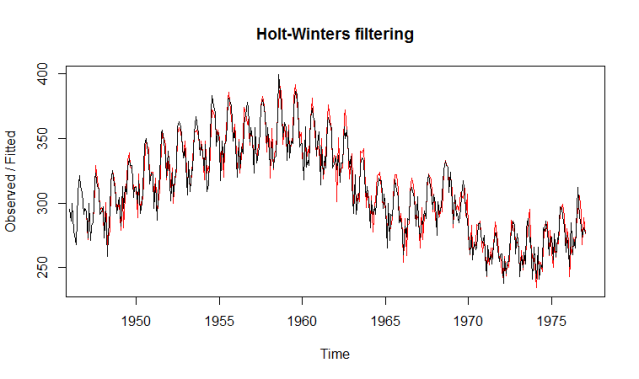
> plot(birthtimeseriesforecasts)

 

 

We see from the plot that the Holt-Winters exponential method is very successful in predicting the seasonal peaks, which occur roughly in November every year.

 

To make forecasts for future times not included in the original time series, we use the “forecast.HoltWinters()” function in the “forecast” package. For example, the original data for the monthly live births (adjusted) in thousands for the United States, is from January 1946 to January 1977. If we wanted to make forecasts for February 1977 to January 1981 (48 more months), and plot the forecasts, we would type:

 

> birthtimeseriesforecasts2 plot.forecast(birthtimeseriesforecasts2)

 

 

The forecasts are shown as a blue line, and the gray and light gray shaded areas show 80% and 95% prediction intervals, respectively.

 

We can investigate whether the predictive model can be improved upon by checking whether the in-sample forecast errors show non-zero autocorrelations at lags 1-20, by making a correlogram and carrying out the Ljung-Box test:

 

> acf(birthtimeseriesforecasts2$residuals, lag.max=30)
> Box.test(birthtimeseriesforecasts2$residuals, lag=30, type="Ljung-Box")
Box-Ljung test
data: birthtimeseriesforecasts2$residuals
X-squared = 81.1214, df = 30, p-value = 1.361e-06

 

 

The correlogram shows that the autocorrelations for the in-sample forecast errors do not exceed the significance bounds for lags 1-20. Furthermore, the p-value for Ljung-Box test is 0.6, indicating that there is little evidence of non-zero autocorrelations at lags 1-20.

 

We can check whether the forecast errors have constant variance over time, and are normally distributed with mean zero, by making a time plot of the forecast errors and a histogram (with overlaid normal curve):

 

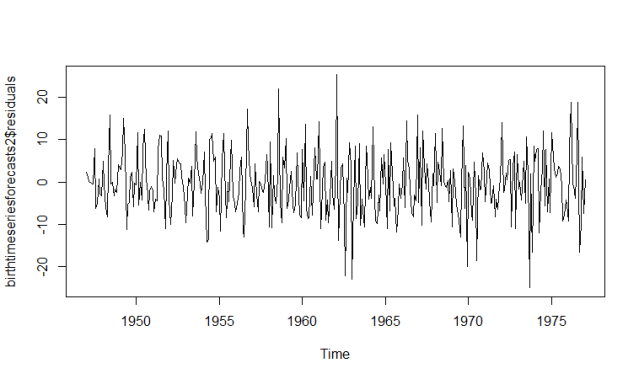
> plot.ts(birthtimeseriesforecasts2$residuals)           # make a time plot
> plotForecastErrors(birthtimeseriesforecasts2$residuals) # make a histogram

 

 

From the time plot, it appears plausible that the forecast errors have constant variance over time. From the histogram of forecast errors, it seems plausible that the forecast errors are normally distributed with mean zero.

 

Thus, there is little evidence of autocorrelation at lags 1-20 for the forecast errors, and the forecast errors appear to be normally distributed with mean zero and constant variance over time. This suggests that Holt-Winters exponential smoothing provides an adequate predictive model of the monthly live births (adjusted) in thousands for the United States, 1946-1979, which probably cannot be improved upon. Furthermore, the assumptions upon which the prediction intervals were based are probably valid.

 

---

Authored by: Jeffrey Strickland, Ph.D.

Jeffrey Strickland, Ph.D., is the Author of “Predictive Analytics Using R” and a Senior Analytics Scientist with Clarity Solution Group. He has performed predictive modeling, simulation and analysis for the Department of Defense, NASA, the Missile Defense Agency, and the Financial and Insurance Industries for over 20 years. Jeff is a Certified Modeling and Simulation professional (CMSP) and an Associate Systems Engineering Professional. He has published nearly 200 blogs on LinkedIn, is also a frequently invited guest speaker and the author of 20 books including:

• Operations Research using Open-Source Tools
• Discrete Event simulation using ExtendSim
• Crime Analysis and Mapping
• Missile Flight Simulation
• Mathematical Modeling of Warfare and Combat Phenomenon
• Predictive Modeling and Analytics
• Using Math to Defeat the Enemy
• Verification and Validation for Modeling and Simulation
• Simulation Conceptual Modeling
• System Engineering Process and Practices
• Weird Scientist: the Creators of Quantum Physics
• Albert Einstein: No one expected me to lay a golden eggs
• The Men of Manhattan: the Creators of the Nuclear Era
• Fundamentals of Combat Modeling
• LinkedIn Memoirs
• Quantum Phaith
• Dear Mister President
• Handbook of Handguns
• Knights of the Cross: The True Story of the Knights Templar

Connect with Jeffrey StricklandContact Jeffrey Strickland

What is Time-Series Analysis, Part 1

This article first appeared on bicorner.com

This article shows you how to use the R statistical software to carry out some simple analyses that are common in analyzing time series data. If the reader has some basic knowledge of time series analysis it will serve them well since the principal focus of the article is not to explain time series analysis, but rather to explain how to carry out these analyses using R.

 

Sometimes the time series data set that you have may have been collected at regular intervals that were less than one year, for example, monthly or quarterly. In this case, you can specify the number of times that data was collected per year by using the ‘frequency’ parameter in the ts() function. For monthly time series data, you set frequency=12, while for quarterly time series data, you set frequency=4.

You can also specify the first year that the data was collected, and the first interval in that year by using the ‘start’ parameter in the ts() function. For example, if the first data point corresponds to the second quarter of 1986, you would set start=c(1986,2).

 

An example is a data set of the monthly live births (adjusted) in thousands for the United States, 1946-1979. The set ‘birth’ is part of the astsa package.

> require(astsa)
> birth ## monthly live births (adjusted) in thousands for the United States, 1946-1979.

Once you have read the time series data into R, the next step is to store the data in a time series object in R, so that you can use R’s many functions for analyzing time series data. To store the data in a time series object, we use the ts() function in R. For example, to store the data in the variable ‘birth’ as a time series object in R, we type:

< birthtimeseries < birthtimeseries
     Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1946 295 286 300 278 272 268 308 321 313 308 291 296
1947 294 273 300 271 282 285 318 323 313 311 291 293
1948 297 273 294 259 276 294 316 325 315 312 292 301
1949 304 282 313 296 313 307 328 334 329 329 304 312
1950 312 300 317 292 300 311 345 350 344 336 315 323
1951 322 296 315 287 307 321 354 356 348 334 320 340
1952 332 302 324 305 318 329 359 363 359 352 335 342
1953 329 306 332 309 326 325 354 367 362 354 337 345
1954 339 325 345 309 315 334 370 383 375 370 344 355
1955 346 317 348 331 345 348 380 381 377 376 348 356
1956 344 320 347 326 343 338 361 368 378 374 347 358
1957 349 323 358 331 338 343 374 380 377 368 346 358
1958 338 329 347 327 335 336 370 399 385 368 351 362
1959 358 333 356 335 348 346 374 386 384 372 343 346
1960 346 318 359 328 333 329 366 373 367 363 337 346
1961 355 314 343 322 336 327 362 366 361 358 327 330
1962 336 326 337 316 331 331 359 350 356 347 328 336
1963 315 292 322 291 302 310 330 335 333 318 305 313
1964 301 281 302 291 297 291 311 319 317 317 296 307
1965 295 265 300 271 291 290 310 318 310 304 285 288
1966 277 260 282 274 288 287 308 312 306 304 282 305
1967 284 273 286 284 294 288 315 322 317 309 295 306
1968 300 275 301 292 298 306 326 332 329 328 308 324
1969 299 284 306 290 292 285 295 306 317 305 294 287
1970 278 261 275 256 270 264 265 284 284 275 269 275
1971 259 244 267 255 260 253 267 277 277 264 255 260
1972 261 238 257 246 254 255 273 276 286 283 261 276
1973 264 243 259 250 262 253 280 288 270 273 241 266
1974 257 242 266 241 252 250 281 278 286 278 260 272
1975 274 256 276 259 273 272 297 296 290 282 262 275
1976 262 251 285 260 272 265 296 312 289 282 274 281
1977 277

Plotting Time Series

Once you have read a time series into R, the next step is usually to make a plot of the time series data, which you can do with the plot.ts() function in R. To plot the time series of the monthly live births (adjusted) in thousands for the United States, we type:

< plot.ts(birthtimeseries)

We can see from this time series that there seems to be seasonal variation in the number of births per month: there is a peak every summer, and a trough every winter. Again, it seems that this time series could probably be described using an additive model, as the seasonal fluctuations are roughly constant in size over time and do not seem to depend on the level of the time series, and the random fluctuations also seem to be roughly constant in size over time.

Decomposing Seasonal Data

A seasonal time series consists of a trend component, a seasonal component and an irregular component. Decomposing the time series means separating the time series into these three components: that is, estimating these three components.

 

To estimate the trend component and seasonal component of a seasonal time series that can be described using an additive model, we can use the “decompose()” function in R. This function estimates the trend, seasonal, and irregular components of a time series that can be described using an additive model.

The function “decompose()” returns a list object as its result, where the estimates of the seasonal component, trend component and irregular component are stored in named elements of that list objects, called “seasonal”, “trend”, and “random” respectively.

 

For example, as discussed above, the time series of the monthly live births (adjusted) in thousands for the United States is seasonal with a peak every summer and trough every winter, and can probably be described using an additive model since the seasonal and random fluctuations seem to be roughly constant in size over time:

> birthtimeseriescomponents

The estimated values of the seasonal, trend and irregular components are now stored in variables birthtimeseriescomponents$seasonal, birthtimeseriescomponents$trend and birthtimeseriescomponents$random. For example, we can print out the estimated values of the seasonal component by typing:

> birthtimeseriescomponents$seasonal # get the estimated values of the seasonal component
Jan   Feb   Mar   Apr   May   Jun   Jul   Aug   Sep   Oct   Nov   Dec
1946  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1947  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1948  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1949  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1950  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1951  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1952  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1953  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1954  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1955  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1956  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1957  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1958  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1959  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1960  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1961  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1962  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1963  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1964  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1965  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1966  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1967  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1968  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1969  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1970  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1971  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1972  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1973  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1974  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1975  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1976  -4.3 -25.1  -1.1 -21.6  -9.9  -9.2  16.5  23.6  20.2  13.8  -6.2   3.2
1977  -4.3

The estimated seasonal factors are given for the months January-December, and are the same for each year. The largest seasonal factor is for August (about 23.6), and the lowest is for February (about -25.1), indicating that there seems to be a peak in births in July and a trough in births in February each year.

 

We can plot the estimated trend, seasonal, and irregular components of the time series by using the “plot()” function, for example:

> plot(birthtimeseriescomponents)
 

The plot below shows the original time series (top), the estimated trend component (second from top), the estimated seasonal component (third from top), and the estimated irregular component (bottom). We see that the estimated trend component shows a small increase from about 300 in 1947 to about 360 in 1959, followed by a steady decrease from then on to about 280 in 1966, followed by a slight increase to about 320 in 1969, followed by a steady decease to about 260 from about 1971 through 1974 and the a slight increase to about 280 in 1979.

Seasonally Adjusting

If you have a seasonal time series that can be described using an additive model, you can seasonally adjust the time series by estimating the seasonal component, and subtracting the estimated seasonal component from the original time series. We can do this using the estimate of the seasonal component calculated by the “decompose()” function.

 

For example, to seasonally adjust the time series of the number of births per month in New York city, we can estimate the seasonal component using “decompose()”, and then subtract the seasonal component from the original time series:

> birthtimeseriescomponents > birthtimeseriesseasonallyadjusted

We can then plot the seasonally adjusted time series using the “plot()” function, by typing:

> plot(birthtimeseriesseasonallyadjusted)

You can see that the seasonal variation has been removed from the seasonally adjusted time series. The seasonally adjusted time series now just contains the trend component and an irregular component.

Forecasts using Exponential Smoothing

Exponential smoothing can be used to make short-term forecasts for time series data.

Simple Exponential Smoothing

If you have a time series that can be described using an additive model with constant level and no seasonality, you can use simple exponential smoothing to make short-term forecasts.

 

The simple exponential smoothing method provides a way of estimating the level at the current time point. Smoothing is controlled by the parameter alpha; for the estimate of the level at the current time point. The value of alpha; lies between 0 and 1. Values of alpha that are close to 0 mean that little weight is placed on the most recent observations when making forecasts of future values.

To make forecasts using simple exponential smoothing in R, we can fit a simple exponential smoothing predictive model using the “HoltWinters()” function in R. To use HoltWinters() for simple exponential smoothing, we need to set the parameters beta=FALSE and gamma=FALSE in the HoltWinters() function (the beta and gamma parameters are used for Holt’s exponential smoothing, or Holt-Winters exponential smoothing, as described below).

 

The HoltWinters() function returns a list variable, that contains several named elements.

For example, to use simple exponential smoothing to make forecasts for the time series of monthly live births (adjusted) in thousands for the United States, 1946-1979, we type:

## Holt-Winters exponential smoothing without trend and without seasonal component.> birthtimeseriesforecasts > birthtimeseriesforecasts
Call:
HoltWinters(x = birthtimeseries, beta = FALSE, gamma = FALSE)
Smoothing parameters:
  alpha: 0.71
  beta : FALSE
  gamma: FALSE
Coefficients:
  [,1]
a  278

The output of HoltWinters() tells us that the estimated value of the alpha parameter is about 0.71. This is very close to zero, telling us that the forecasts are based on both recent and less recent observations (although somewhat more weight is placed on recent observations).

 

By default, HoltWinters() just makes forecasts for the same time period covered by our original time series. In this case, our original time series included monthly live births (adjusted) in thousands for the United States, 1948-1979.

 

In the example above, we have stored the output of the HoltWinters() function in the list variable “birthstimeseriesforecasts”. The forecasts made by HoltWinters() are stored in a named element of this list variable called “fitted”, so we can get their values by typing:

> birthtimeseriesforecasts $fitted
xhat level
Feb 1946  295   295
Mar 1946  289   289
Apr 1946  297   297
May 1946  283   283
Jun 1946  275   275
Jul 1946  270   270
Aug 1946  297   297
Sep 1946  314   314
Oct 1946  313   313
Nov 1946  310   310
Dec 1946  296   296
Jan 1947  296   296
Feb 1947  295   295
Mar 1947  279   279
Apr 1947  294   294
May 1947  278   278
Jun 1947  281   281
Jul 1947  284   284
Aug 1947  308   308
Sep 1947  319   319
Oct 1947  315   315
Nov 1947  312   312
Dec 1947  297   297
.
.
.
Jan 1976  273   273
Feb 1976  265   265
Mar 1976  255   255
Apr 1976  276   276
May 1976  265   265
Jun 1976  270   270
Jul 1976  266   266
Aug 1976  287   287
Sep 1976  305   305
Oct 1976  294   294
Nov 1976  285   285
Dec 1976  277   277
Jan 1977  280   280

We can plot the original time series against the forecasts by typing:

> plot(birthtimeseriesforecasts)

The plot shows the original time series in black, and the forecasts as a red line. The time series of forecasts is much smoother than the time series of the original data here.

As a measure of the accuracy of the forecasts, we can calculate the sum of squared errors for the in-sample forecast errors, that is, the forecast errors for the time period covered by our original time series. The sum-of-squared-errors is stored in a named element of the list variable “birthtimeseriesforecasts” called “SSE”, so we can get its value by typing:

> birthtimeseriesforecasts$SSE
[1] 97559

That is, here the sum-of-squared-errors is 97559.

It is common in simple exponential smoothing to use the first value in the time series as the initial value for the level. For example, in the time series for monthly live births (adjusted) in thousands for the United States, 1946-1979, the first value is 295 in 1946. You can specify the initial value for the level in the HoltWinters() function by using the “l.start” parameter. For example, to make forecasts with the initial value of the level set to 295, we type:

> HoltWinters(birthtimeseries, beta=FALSE, gamma=FALSE, l.start=295)

As explained above, by default HoltWinters() just makes forecasts for the time period covered by the original data, which is 1946-1979 for the birth time series. We can make forecasts for further time points by using the “forecast.HoltWinters()” function in the R “forecast” package. To use the forecast. HoltWinters() function, we first need to install the “forecast” R package (for instructions on how to install an R package, see How to install an R package).

Once you have installed the “forecast” R package, you can load the “forecast” R package by typing:

> library("forecast")

When using the forecast.HoltWinters() function, as its first argument (input), you pass it the predictive model that you have already fitted using the HoltWinters() function. For example, in the case of the birth time series, we stored the predictive model made using HoltWinters() in the variable “birthstimeseriesforecasts”. You specify how many further time points you want to make forecasts for by using the “h” parameter in forecast.HoltWinters(). For example, to make a forecast of births for the years Feb 1977 to Sep 1978 (8 more months) using forecast.HoltWinters(), we type:

> birthtimeseriesforecasts2 > birthtimeseriesforecasts2 Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
Feb 1977            278   257   299   246   310
Mar 1977            278   252   303   239   317
Apr 1977            278   248   307   233   323
May 1977            278   245   311   227   328
Jun 1977            278   242   314   223   333
Jul 1977            278   239   317   218   338
Aug 1978            278   236   320   214   342
Sep 1978            278   234   322   210   346

The forecast.HoltWinters() function gives you the forecast for a year, a 80% prediction interval for the forecast, and a 95% prediction interval for the forecast. For example, the forecasted births for 1979 is about 275 births, with a 95% prediction interval of (250, 320).

 

To plot the predictions made by forecast.HoltWinters(), we can use the “plot.forecast()” function:

> plot.forecast(birthtimeseriesforecasts2)

Here the forecasts for 1946-1979 are plotted as a blue line, the 80% prediction interval as a gray shaded area, and the 95% prediction interval as a light gray shaded area.

The ‘forecast errors’ are calculated as the observed values minus predicted values, for each time point. We can only calculate the forecast errors for the time period covered by our original time series, which is 1946-1979 for the birth data. As mentioned above, one measure of the accuracy of the predictive model is the sum-of-squared-errors (SSE) for the in-sample forecast errors.

The in-sample forecast errors are stored in the named element “residuals” of the list variable returned by forecast.HoltWinters(). If the predictive model cannot be improved upon, there should be no correlations between forecast errors for successive predictions. In other words, if there are correlations between forecast errors for successive predictions, it is likely that the simple exponential smoothing forecasts could be improved upon by another forecasting technique.

 

To figure out whether this is the case, we can obtain a correlogram of the in-sample forecast errors for lags 1-20. We can calculate a correlogram of the forecast errors using the “acf()” function in R. To specify the maximum lag that we want to look at, we use the “lag.max” parameter in acf().

For example, to calculate a correlogram of the in-sample forecast errors for the birth data for lags 0-30, we type:

> acf(birthtimeseriesforecasts2$residuals, lag.max=30)

You can see from the sample correlogram that the autocorrelation at lag 0 is just crosses the significance bounds. To test whether there is significant evidence for non-zero correlations at lags 1-30, we can carry out a Ljung-Box test. This can be done in R using the “Box.test()”, function. The maximum lag that we want to look at is specified using the “lag” parameter in the Box.test() function. For example, to test whether there are non-zero autocorrelations at lags 1-30, for the in-sample forecast errors for monthly live births for the United States data (1946-1977), we type:

> Box.test(birthtimeseriesforecasts2$residuals, lag=20, type="Ljung-Box")          Box-Ljung test
data:  birthtimeseriesforecasts2$residuals
X-squared = 470, df = 20, p-value < 2.2e-16

Here the Ljung-Box test statistic is 470, and the p-value is 0.001, so there is evidence of non-zero autocorrelations in the in-sample forecast errors at lags 1-30.

 

To be sure that the predictive model cannot be improved upon, it is also a good idea to check whether the forecast errors are normally distributed with mean zero and constant variance. To check whether the forecast errors have constant variance, we can make a time plot of the in-sample forecast errors:

> plot.ts(birthtimeseriesforecasts2$residuals)

The plot shows that the in-sample forecast errors seem to have roughly constant variance over time, although the size of the fluctuations in the start of the time series (1846-1861) may be slightly less than that at later dates (e.g., 1862-1877).

 

To check whether the forecast errors are normally distributed with mean zero, we can plot a histogram of the forecast errors, with an overlaid normal curve that has mean zero and the same standard deviation as the distribution of forecast errors. To do this, we can define an R function “plotForecastErrors()”, below:

> plotForecastErrors function(forecasterrors)
{ 
# make a histogram of the forecast errors:   mybinsize    mysd    mymin    mymax    # generate normally distributed data with mean 0 and standard deviation mysd   mynorm    mymin2    mymax2       if (mymin2 < mymin) { mymin       if (mymax2 > mymax) { mymax    # make a red histogram of the forecast errors, with the normally distributed data overlaid:   mybins    hist(forecasterrors, col="red", freq=FALSE, breaks=mybins)
   # freq=FALSE ensures the area under the histogram = 1
   # generate normally distributed data with mean 0 and standard deviation mysd
   myhist FALSE, breaks=mybins)  
   # plot the normal curve as a blue line on top of the histogram of forecast errors:
   points(myhist$mids, myhist$density, type="l", col="blue", lwd=2)
}

You will have to copy the function above into R in order to use it. You can then use plotForecastErrors() to plot a histogram (with overlaid normal curve) of the forecast errors for the birth predictions:

> plotForecastErrors(birthtimeseriesforecasts2$residuals)

The plot shows that the distribution of forecast errors is roughly centered on zero, and is more or less normally distributed, although it seems to be slightly skewed to the right compared to a normal curve. However, the right skew is relatively small, and so it is plausible that the forecast errors are normally distributed with mean zero.

The Ljung-Box test showed that there is little evidence of non-zero autocorrelations in the in-sample forecast errors, and the distribution of forecast errors seems to be normally distributed with mean zero. This suggests that the simple exponential smoothing method provides an adequate predictive model for the births for the United States data (1946-1977), which probably cannot be improved upon. Furthermore, the assumptions that the 80% and 95% predictions intervals were based upon (that there are no autocorrelations in the forecast errors, and the forecast errors are normally distributed with mean zero and constant variance) are probably valid.

---

Authored by: Jeffrey Strickland, Ph.D.

Jeffrey Strickland, Ph.D., is the Author of “Predictive Analytics Using R” and a Senior Analytics Scientist with Clarity Solution Group. He has performed predictive modeling, simulation and analysis for the Department of Defense, NASA, the Missile Defense Agency, and the Financial and Insurance Industries for over 20 years. Jeff is a Certified Modeling and Simulation professional (CMSP) and an Associate Systems Engineering Professional. He has published nearly 200 blogs on LinkedIn, is also a frequently invited guest speaker and the author of 20 books including:

• Operations Research using Open-Source Tools
• Discrete Event simulation using ExtendSim
• Crime Analysis and Mapping
• Missile Flight Simulation
• Mathematical Modeling of Warfare and Combat Phenomenon
• Predictive Modeling and Analytics
• Using Math to Defeat the Enemy
• Verification and Validation for Modeling and Simulation
• Simulation Conceptual Modeling
• System Engineering Process and Practices
• Weird Scientist: the Creators of Quantum Physics
• Albert Einstein: No one expected me to lay a golden eggs
• The Men of Manhattan: the Creators of the Nuclear Era
• Fundamentals of Combat Modeling
• LinkedIn Memoirs
• Quantum Phaith
• Dear Mister President
• Handbook of Handguns
• Knights of the Cross: The True Story of the Knights Templar

Connect with Jeffrey StricklandContact Jeffrey Strickland

Where Did All The Thinking Go?

 

Some people are saying that statistical methods in data science and analytics are obsolete. These people have either just grown tired of thinking or have forgotten how to.

What is wrong with this picture?

This view has two major problems. First, espousing the idea that machine learning algorithms is the only method required for providing analytic solutions to business problems is a very naïve view. Second, this idea is philosophically dangerous and reeks with an undertone of quantitative inadequacy.

How can you be so naïve?

Naïve is being kind. What you really have is extreme arrogance. You have some people that practically no one has ever heard of, essentially saying they are smarter than the late George Box, who is not here to defend himself. They apparently know more about probability and statistics than Andrey Kolmogorov, Nikolai Smirnov, Andrey Markov, Richard Jeffrey, Adrien-Marie Legendre, John Herschel, Friedrich Bessel and Richard Cox. They want o throw away statistical models and only use machine learning algorithms, which reminds me of the King James version only movement. What I really see is a desperate cry of “We do not understand mathematics, probability or statistics, so we’ll assume it away.”

Why is this dangerous?

To me this is a no brainer, but those who propose this seem to be brainless. We (in the United States) already have a math-phobic society and an educational system that is substandard relative to many other countries. As if we have not dumbed down quantitative skills enough, we add the “for Dummies” series to add salt to the wound.

 

It seems that undergraduate programs are teaching tools, and when you ask a recent graduate to solve a real problem with a customer's licensed tool, you may hear, “Can I do it in MATLAB? That’s what I know.” We tend to want to force every problem into our favorite tool or technique, rather than solve the problem with the appropriate tool, or actually think.

 

The cry is, “Give me a tool that does not require me to apply much thought in order to use!” And many are providing such tools, along with courses to learn them, and making lots of money in the process. What we get is a society of people who do not have any critical thinking skills. Moreover, critical thinking skills are not only required for the quantitative sciences, but also in disciplines like biology (my undergraduate degree) as well. Though I am not a great writer, I am critically thinking about sentence structure, grammar, logic and so on, as I write.

Can Machines Think?

Alan Turing said they could, but he qualified his statement by saying they think differently than humans. Roger Penrose basically said “Ditto” when addressing artificial intelligence. So, are machine learning algorithms the way to solve problems? Certainly, except they are not the only way, as some might propose. If you are trying to solve a problem where all the assumptions of a linear program are met, will a genetic algorithm give a better answer? Not necessarily and probably not.

There has to be a decision process involved in choosing the best functional form for solving various problems. Decision points, like whether or not data pathologies exist, have to be weighed. Generally, if the assumptions of traditional methods are not violated, they usually yield the best results. Do an experiment. Take a problem were all the assumption of a logistic regression are met and compare the results with an artificial neural network. I performed such an experiment with a real business problem and two different logistic regression models outperformed a neural network. However, when used together in an ensemble, the logistic regression and neural network combination (using averaging) outperformed everything else in performance testing. In very simple terms, this takes the strengths of both and negates the weaknesses of either.

I also checked the results of a logistic regression uplift model built in SAS by employing a random forest in R. Although the distribution among pentile was a little different, the overall net lift was the same. So, I am not saying that machine learning algorithms should not be used, only that some logic has to be used for selecting them as the functional form of your solution method.

Should Humans Think?

They should, but there seems to be a growing thesis to not do so. “I don’t want to think!” “It makes my brain hurt!” When solving problems, we usually examine the “What” or the “So what”. However, the “Why”, though it may not be important for the business owner, should be important to the analyst. Anytime our methods produce answers, we should be asking “Why?” (and probably “How?”). I would never give my customer a solution without knowing the “Why” and the “How”. I may never be asked questions that requires my understanding of either, but as the analyst, I have to know.

 

If my solution method is a black-box, I must try to make it as “gray” as possible. One of the things we have a tendency to do is forget intuition as a legitimate problem solving process. When I produce a solution through the logical approach, I have to ask, “Does this intuitively make sense?” Does the period required for underwriting have a bearing on a decision to buy insurance from company X? Does the possession of a reward card from Citibank have a bearing on a decision to buy insurance from company X? There latter is not so intuitively clear, but we have to know why the relation exists.

Conclusion

If we were asked to build a house, would we show up with just a screwdriver? Probably not. We wound bring our complete set of tools to bear. If we were asked to make a decision for financing our new home with a mortgage, would we choose the type and mortgage company at random? Would you force the problem into a model with an unsupervised learning algorithm? (You would probably just ask who has the lowest interest rate.)

The analysis of data should produce information that is useful for making a decision. Yet, that is not all of the information. This is the fallacy of taking “Human” out of HR. When we screen every resume with software and reject some based on certain criteria, are we possibly eliminating the very best candidate for the job? The human element must be involved in decisions, no matter what the question is or in what discipline it occurs. Blindly accepting solutions is naïve and dangerous. Believing you know better than George Box is arrogant.

“All models are wrong; but some are useful”

—George Box

About The Author

Serving in the military for 24 years as a cavalry unit officer and operations research analyst, Jeffrey Strickland has been applying quantitative methods in decision making for 34 years. He has been involved in the design of long-range unmanned aerial vehicles (UAV), manned space launch systems, missile defense systems, satellite systems, and communication systems. He has developed models for predicting combat outcomes, weapon systems effectiveness, vulnerability to cyber-attacks, occurrences of crime, propensity to purchase, propensity to engage, and propensity to churn. He holds a Masters and Doctorate in Mathematics and is a Certified Modeling and Simulation Professional (CMSP). Jeffrey has published over 20 technical books and written over 300 articles and blogs.